题目内容
函数f(x)=![]() 其中P、M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M},给出下列四个判断:①若P∩M=
其中P、M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M},给出下列四个判断:①若P∩M=![]() ,则f(P)∩f(M)=
,则f(P)∩f(M)=![]() ;②若P∩M≠
;②若P∩M≠![]() ,则f(P)∩f(M)≠
,则f(P)∩f(M)≠![]() ;③若P∪M=R,则f(P)∪f(M)=R;④若P∪M≠R,则f(P)∪f(M)≠R.其中正确判断有
;③若P∪M=R,则f(P)∪f(M)=R;④若P∪M≠R,则f(P)∪f(M)≠R.其中正确判断有
[ ]
A.1个
B.2个
C.3个
D.4个
答案:B
解析:
提示:
解析:
|
解析:若取P={1,2},M={-2,-1},则f(P)={1,2},f(M)={1,2},f(P)∩f(M)={1,2}≠ |
提示:
|
本题主要考查了集合与函数的有关知识的分析判断能力.要否定一个命题,只需举出一个反例. |

练习册系列答案
相关题目
 }的前二项和为
}的前二项和为 ,
, 为不共线向量,又
为不共线向量,又 ,
, ,则S2012=1006.
,则S2012=1006. 是函数
是函数 的最小正周期为4"的充要条件;
的最小正周期为4"的充要条件; }的前二项和为
}的前二项和为 ,
, 为不共线向量,又
为不共线向量,又 ,
, ,则S2012=1006.
,则S2012=1006. 是函数
是函数 的最小正周期为4"的充要条件;
的最小正周期为4"的充要条件;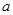 无限趋近于0时,
无限趋近于0时,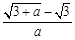 无限趋近于
无限趋近于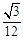 ;
;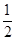 ”的必要不充分。
”的必要不充分。