题目内容
已知函数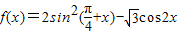 .
.(1)将f(x)的解析基本功化成Asin(ωx+φ)+b的形式,并求函数f(x)图象离y轴最近的对称轴的方程;
(2)求函数
 内的值域.
内的值域.
【答案】分析:(1)先根据二倍角公式与和角公式化简解析式,再由正弦函数的对称性求其对称轴即可
(2)借助(1)中化简后的解析式,利用正弦函数的单调性求函数 的值域即可
的值域即可
解答:解:(1)由题意 =1+sin2x-
=1+sin2x- cos2x=1+2sin(2x-
cos2x=1+2sin(2x- )
)
令2x- =kπ+
=kπ+ ,得x=
,得x= ,当k=-1时,|x|的值最小,
,当k=-1时,|x|的值最小,
故函数f(x)图象离y轴最近的对称轴的方程是x=-
(2)当 时2x-
时2x- ∈
∈ ,2sin(2x-
,2sin(2x- )
)
故函数 内的值域为
内的值域为
点评:本题考点是三角函数的恒等变换以及正弦函数的对称性、正弦函数的单调性,属于三角函数性质的基本运用题,解答本题要注意三角函数值域的求法步骤.
(2)借助(1)中化简后的解析式,利用正弦函数的单调性求函数
 的值域即可
的值域即可解答:解:(1)由题意
 =1+sin2x-
=1+sin2x- cos2x=1+2sin(2x-
cos2x=1+2sin(2x- )
)令2x-
 =kπ+
=kπ+ ,得x=
,得x= ,当k=-1时,|x|的值最小,
,当k=-1时,|x|的值最小,故函数f(x)图象离y轴最近的对称轴的方程是x=-

(2)当
 时2x-
时2x- ∈
∈ ,2sin(2x-
,2sin(2x- )
)
故函数
 内的值域为
内的值域为
点评:本题考点是三角函数的恒等变换以及正弦函数的对称性、正弦函数的单调性,属于三角函数性质的基本运用题,解答本题要注意三角函数值域的求法步骤.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
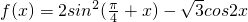 .
.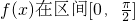 内的值域.
内的值域.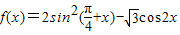 .
. 内的值域.
内的值域.