题目内容
设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明:对一切正整数n,有 +
+ +…+
+…+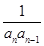 <
<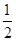 .
.
(Ⅰ) ;(Ⅱ)详见解析
;(Ⅱ)详见解析
解析试题分析:(Ⅰ)利用等差数列的通项公式和前 项和公式来求;(Ⅱ)裂项求和.
项和公式来求;(Ⅱ)裂项求和.
试题解析:(Ⅰ)设等差数列{an}的公差为d,则 ,解得
,解得
∴an=2n-1,n∈N*. 6分
(Ⅱ)∵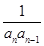 =
= =
=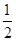 (
( -
- ),
),
∴ +
+ ++
++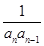
=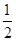 [(1-
[(1- )+(
)+( -
- )++(
)++( -
- )]
)]
=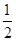 (1-
(1- )<
)<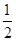 . 12分
. 12分
考点:等差数列的通项公式和前 项和公式,裂项求和.
项和公式,裂项求和.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,公差
,公差 不为零,
不为零,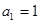 ,且
,且 成等比数列;
成等比数列; 满足
满足 ,求数列
,求数列 项和
项和 .
.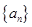 满足:
满足: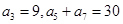 ,
,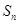 .
.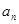 及
及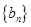 的第n项为
的第n项为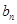 ,若
,若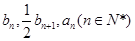 成等差数列,且
成等差数列,且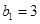 ,设数列
,设数列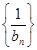 的前
的前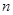 项和
项和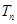 .求数列
.求数列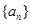 的前
的前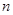 项和为
项和为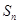 ,
,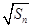 是
是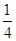 与
与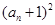 的等比中项.
的等比中项.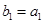 ,且
,且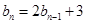 ,求数列
,求数列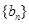 的通项公式;
的通项公式;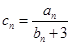 ,求数列
,求数列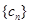 的前
的前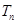 .
. 的前n项和为
的前n项和为 ,
, 和
和 满足等式
满足等式
 的值;
的值; 是等差数列;
是等差数列; 满足
满足 ,求数列
,求数列 ;
; ,求证:
,求证:
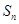 是数列
是数列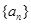 的前
的前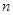 项和,
项和,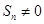 ,
,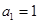 ,
,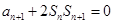 .
.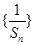 是等差数列,并
是等差数列,并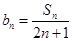 ,求数列
,求数列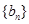 的前
的前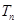 .
.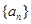 、
、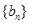 满足
满足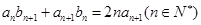 .
.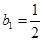 时,求数列
时,求数列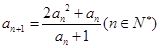 ,
,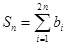 ,求证:
,求证: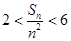 .
. .
.
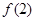 ,
,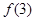 ,
,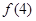 ,
,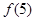 ;
;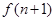 的关系,并求出
的关系,并求出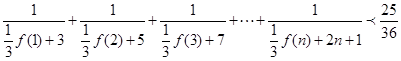 (
( ).
).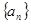 中,已知
中,已知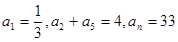 ,试求n的值
,试求n的值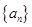 中,
中,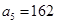 ,公比
,公比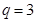 ,前
,前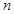 项和
项和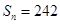 ,求首项
,求首项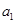 和项数
和项数