题目内容
已知函数 ,
, .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)在 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且满足
,且满足 ,
,
求 的值.
的值.
(1) ;(2)
;(2) .
.
解析试题分析:(1)首先化简已知函数的解析式为 ,则可得到函数的周期为
,则可得到函数的周期为 ;(2)应用余弦定理将已知等式:
;(2)应用余弦定理将已知等式: 中的
中的 转化为只含边的等式,可求得角B的余弦值,进而就可求得角B的具体值,然后代入
转化为只含边的等式,可求得角B的余弦值,进而就可求得角B的具体值,然后代入 的解析式中即可求得
的解析式中即可求得 的值.另也可利用正弦定理将已知等式:
的值.另也可利用正弦定理将已知等式: 转化为只有角的关系式:
转化为只有角的关系式: 再用三角恒等变形公式同样可求出角B的大小.
再用三角恒等变形公式同样可求出角B的大小.
试题解析:(1) .......2分
.......2分 函数
函数 的最小正周期
的最小正周期 ; 4分
; 4分
(2)解法一: , 6分
, 6分
整理得 ,
,
故 , 9分
, 9分 ,
, ,
, ; 12分
; 12分
解法二: ,
, ,
, ,
, ,
, ,
, ,
, .
.
考点:1.三角恒等变形公式;2.三角函数的性质;3.余弦定理.

练习册系列答案
相关题目
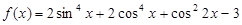 .
.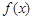 的最小正周期.
的最小正周期.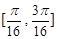 上的最小值并求当
上的最小值并求当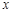 的取值集合.
的取值集合.




 (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π. 上的单调性.
上的单调性. <j<
<j< ,
, 时,求f(x)的取值范围.
时,求f(x)的取值范围. 上的函数y=f(x)的图象关于直线x=-
上的函数y=f(x)的图象关于直线x=- 对称,当x∈
对称,当x∈ 时,函数f(x)=Asin(ωx+φ)
时,函数f(x)=Asin(ωx+φ) 的图象如图所示.
的图象如图所示.
 的解.
的解. ______________.
______________. =
=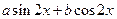 ,其中a,b
,其中a,b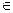 R,ab
R,ab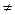 0,若
0,若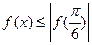 对一切则x
对一切则x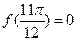 ;②
;②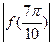 <
<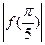 ;③
;③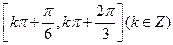 ;⑤存
;⑤存 ,
, ,则
,则
 .
.