题目内容
已知函数
，则下列命题正确的是（ ）A．对任意
，方程f（x）=a只有一个实根B．对任意
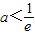，方程f（x）=a总有两个实根C．对任意
，总存在正数x，使得f（x）＞a成立D．对任意
和正数x，总有f（x）＞a成立
【答案】分析：借助于导数求出函数的单调区间，进而得到函数的极值点也是最值点，再逐个验证后即可得正确答案．
解答：解：由于函数
，则
（x＞0）
令
，则1-lnx=0，解得x=e，
当0＜x＜e时，
即函数
在区间（0，e）上为增函数，
当x＞e时，
即函数
在区间（e，+∞）上为减函数．
则函数在x=e时取得最大值，此时
，故C正确
故答案为C．
点评：本题主要考查利用导数来研究函数的性质，属于基础题．
解答：解：由于函数
，则（x＞0）令
，则1-lnx=0，解得x=e，当0＜x＜e时，
即函数在区间（0，e）上为增函数，当x＞e时，
即函数在区间（e，+∞）上为减函数．则函数在x=e时取得最大值，此时
，故C正确故答案为C．
点评：本题主要考查利用导数来研究函数的性质，属于基础题．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
，则下列命题正确的是（ ）
是周期为1的奇函数 （B）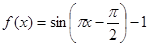
，则下列命题正确的是
（ ）
是周期为1的奇函数 B．
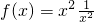，则下列命题中：
，则下列命题中：
．