��Ŀ����
����Ŀ����Ϥ,2017�����������ȫ���г���ģ�Ѵﵽ8.19����Ԫ,�й�ռ��ȫ���г��ݶ�10.8%.ͨ������������õ�40���й�������������ҵ,��ͼ��40����ҵ�����˵IJ�ֵƵ�ʷֲ�ֱ��ͼ.

��1����![]() ��ֵ��
��ֵ��
��2����������ȡ��40����ҵ����ȡ3�����鵽��ֵС��500��Ԫ����ҵ�����������ĸ����Ƕ��٣�
��3����������ȡ��40����ҵ����ȡ2��,��![]() Ϊ��ֵ������500��Ԫ����ҵ������ȥ����500��Ԫ����ҵ�����IJ�ֵ,��
Ϊ��ֵ������500��Ԫ����ҵ������ȥ����500��Ԫ����ҵ�����IJ�ֵ,��![]() �ķֲ��м�����.
�ķֲ��м�����.
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() .
.
����������������1������Ƶ�ʷֲ�ֱ��ͼ�����ε������Ϊ![]() �ɼ����
�ɼ����![]() .
.
��2������Ƶ�ʷֲ�ֱ��ͼ�������ֵС��500��Ԫ����ҵ��![]() �����������ĸ���Ϊ
�����������ĸ���Ϊ![]() ��
��
��3��![]() ��ȡ
��ȡ![]() �����ó����ηֲ����Լ���
�����ó����ηֲ����Լ���![]() ȡ��ֵ�ĸ��ʣ��Ӷ��õ���ֲ��к�����.
ȡ��ֵ�ĸ��ʣ��Ӷ��õ���ֲ��к�����.
��⣺��1������Ƶ�ʷֲ�ֱ��ͼ��֪��![]() ��
��
��ֵС��500��Ԫ����ҵ����Ϊ��![]() ��
��
���Գ鵽��ֵС��500��Ԫ����ҵ�����������ĸ���Ϊ![]() ��
��
��3��![]() �����п���ȡֵΪ
�����п���ȡֵΪ![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
|
|
|
|
|
|
|
|
������![]() ��
��

����Ŀ��ij���ֽ����г���ij�ͺŵĶ���������ʹ������![]() ��
��![]() �������ۼ۸�
�������ۼ۸�![]() ����λ����Ԫ/���������������õ����µĶ�Ӧ���ݣ�
����λ����Ԫ/���������������õ����µĶ�Ӧ���ݣ�
ʹ������ | 2 | 4 | 6 | 8 | 10 |
���ۼ۸� | 16 | 13 | 9.5 | 7 | 4.5 |
��I������![]() ����
����![]() �Ļع�ֱ�߷���
�Ļع�ֱ�߷���![]() .
.
���ο���ʽ��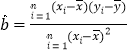 ��
��![]() ��
��
��II����֪ÿ�����ͺ��������չ��۸�Ϊ![]() ��Ԫ�����ݣ�I��������Ļع鷽�̣�Ԥ��
��Ԫ�����ݣ�I��������Ļع鷽�̣�Ԥ��![]() Ϊ��ֵʱ������һ�����ͺ���������õ�����
Ϊ��ֵʱ������һ�����ͺ���������õ�����![]() �������=���ۼ۸�-�չ��۸�
�������=���ۼ۸�-�չ��۸�

