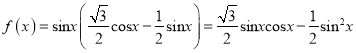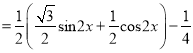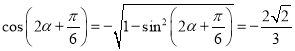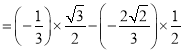题目内容
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
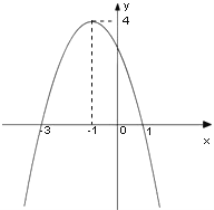
时, ![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴左侧的图象,如图所示,并根据图象:
轴左侧的图象,如图所示,并根据图象:

(1)直接写出函数![]() ,
, ![]() 的增区间;
的增区间;
(2)写出函数![]() ,
, ![]() 的解析式;
的解析式;
(3)若函数![]() ,
, ![]() ,求函数
,求函数![]() 的最小值.
的最小值.
【答案】(1)![]() 在区间
在区间![]() ,
, ![]() 上单调递增;(2)
上单调递增;(2) ;(3)
;(3)![]() 的最小值为
的最小值为 .
.
【解析】试题分析:(1)根据偶函数的图象关于![]() 轴对称,可作出
轴对称,可作出![]() 的图象,由图象可得
的图象,由图象可得![]() 的单调递增函数;
的单调递增函数;
(2)令![]() ,则
,则![]() ,根据条件可得
,根据条件可得![]() ,利用函数
,利用函数![]() 是定义在
是定义在![]() 上的偶函数,可得
上的偶函数,可得![]() ,从而可得函数的解析式;
,从而可得函数的解析式;
(3)先求出抛物线对称轴![]() ,然后分当
,然后分当![]() 时,当
时,当![]() ,当
,当![]() 时三种情况,根据二次函数的增减性解答.
时三种情况,根据二次函数的增减性解答.
试题解析:
(1)![]() 在区间
在区间![]() ,
, ![]() 上单调递增.
上单调递增.
(2)设![]() ,则
,则![]() .
.
∵函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时, ![]() .
.
∴![]()
![]() ,
,
∴ .
.
(3)![]() ,对称轴方程为:
,对称轴方程为: ![]() ,
,
当![]() 时,
时, ![]() 为最小;
为最小;
当![]() 时,
时, ![]() 为最小;
为最小;
当![]() 时,
时, ![]() 为最小.
为最小.
综上,有: ![]() 的最小值为
的最小值为 .
.

练习册系列答案
相关题目