题目内容
已知: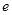 是自然对数的底数,
是自然对数的底数,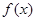 为定义在
为定义在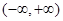 上的可导函数,且
上的可导函数,且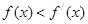 对于
对于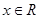 恒成立,则( )
恒成立,则( )
A.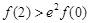 ,
,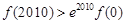 B.
B.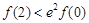 ,
,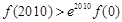
C.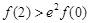 ,
,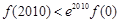 D.
D.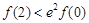 ,
,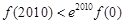
【答案】
A
【解析】
试题分析:∵f(x)<f'(x) 从而 f'(x)-f(x)>0 从而 >0
>0
即[ ]′>0,所以函数y=
]′>0,所以函数y= 单调递增,
单调递增,
故当x>0时, >
> =f(0),整理得出f(x)>exf(0)
=f(0),整理得出f(x)>exf(0)
当x=2时f(2)> f(0),
f(0),
当x=2010时f(2010)>e2010?f(0).故选A。
考点:本题主要考查函数的单调性与其导函数的关系。
点评:中档题,函数在给定区间是增函数,则的函数不小于0;函数在给定区间是减函数,则的函数不大于0;解答本题的关键是结合已知条件,构造函数y= 。
。

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 其中
其中 是自然对数的底 .
是自然对数的底 . 在
在 处取得极值,求
处取得极值,求 的值;
的值;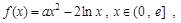 其中
其中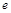 是自然对数的底 .
是自然对数的底 .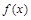 在
在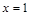 处取得极值,求
处取得极值,求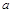 的值;
的值;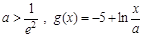 ,存在
,存在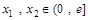 ,使得
,使得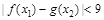 成立,求
成立,求 是自然对数的底)
是自然对数的底) 的单调区间;
的单调区间; 时,若方程
时,若方程 在区间
在区间 上有两个不同的实根,求证:
上有两个不同的实根,求证: 。
。