题目内容
(本小题满分12分)
已知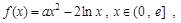 其中
其中 是自然对数的底 .
是自然对数的底 .
(1)若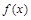 在
在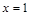 处取得极值,求
处取得极值,求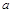 的值;
的值;
(2)求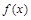 的单调区间;
的单调区间;
(3)设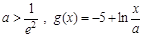 ,存在
,存在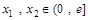 ,使得
,使得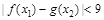 成立,求
成立,求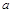 的取值范围.
的取值范围.
【答案】
(Ⅰ)  。(Ⅱ) 综上所述,当
。(Ⅱ) 综上所述,当 时,
时, 的减区间是
的减区间是 ,
,
当 时,
时, 的减区间是
的减区间是 ,增区间是
,增区间是 . (III)
. (III)  .
.
【解析】本试题主要是考查了导数在研究函数性质中的运用,求解极值和单调区间,以及证明不等式的总额和运用。
(1) .
.
由已知 , 解得
, 解得 .
.
(2)因为 ,对于参数a大于零还是小于零,还是等于零分情况讨论得到单调性。
,对于参数a大于零还是小于零,还是等于零分情况讨论得到单调性。
(3)当 时,由(Ⅱ)知
时,由(Ⅱ)知 的最小值是
的最小值是 ;
;
易知 在
在 上的最大值是
上的最大值是 ,则转换为不等式组得到结论。
,则转换为不等式组得到结论。
解: (Ⅰ)  .
.
由已知 , 解得
, 解得 .
.
经检验,  符合题意.
………… 3分
符合题意.
………… 3分
(Ⅱ)  .
.
1)
当 时,
时, 在
在 上是减函数.
上是减函数.
2)当 时,
时, .
.
①
若 ,即
,即 ,
,
则 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
② 若 ,即
,即 ,则
,则 在
在 上是减函数.
上是减函数.
综上所述,当 时,
时, 的减区间是
的减区间是 ,
,
当 时,
时, 的减区间是
的减区间是 ,增区间是
,增区间是 . ……… 7分
. ……… 7分
(III)当 时,由(Ⅱ)知
时,由(Ⅱ)知 的最小值是
的最小值是 ;
;
易知 在
在 上的最大值是
上的最大值是 ;
;
注意到 ,
,
故由题设知
解得 .故
.故 的取值范围是
的取值范围是 .
……… 12分
.
……… 12分

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目