Question

在平面直角坐标系中，直线上有一系列点：，，

，已知数列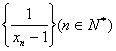是首项为，公差为1的等差数列.

   （Ⅰ）求数列及数列的通项公式；

   （Ⅱ）是否在一个半径最小的圆C，使得对于一切，点均在此圆的内部（包括圆周）？若存在，求由此方程；若不存在，请说明理由.

Answer 1

解：（I）由条件，得

      

      

      

   （II）P₁（3，－1），P₀（1，3），

       以线段P₁P₀为直径作圆D，其圆心D为（2，1）

       则圆D是一个使P₁、P₀在圆的内部（包括圆周）的半径最小的圆.

       圆D的方程为

       ，

       n=0时，P₀D²=5，n=1时，P₁D²=5，

       n≥2时，

       由上可得，圆D即为所求圆C.

       即存在一个半径最小的圆C，使得对于一切均在此圆的内部

（包括圆周）.