题目内容
 在直角梯形ABCD中,∠ABC=∠BAD=90°,BE⊥平面ABCD,AB=BC=BE=2AD=2.
在直角梯形ABCD中,∠ABC=∠BAD=90°,BE⊥平面ABCD,AB=BC=BE=2AD=2.(Ⅰ)求异面直线DE与AC所成角的大小;
(Ⅱ)在线段CE上是否存在点F,使平面BDF⊥平面ADE,若存在,确定点F的位置,若不存在,请说明理由.
分析:先建立空间直角坐标系,写出有关的点及向量的坐标.(Ⅰ)先求出两条异面直线的方向向量,进而利用向量的夹角即可求出异面直线所成的夹角;
(Ⅱ)利用
•
=0?
⊥
,来证明线线垂直,从而证明线面、面面垂直.
(Ⅱ)利用
| a |
| b |
| a |
| b |
解答:解:由于在直角梯形ABCD中,∠ABC=∠BAD=90°,BE⊥平面ABCD,
则AB,BC,BE两两垂直,
故可以B为原点建立如图所示空间直角坐标系B-xyz.

∵AB=BC=BE=2AD=2,
则B(0,0,0),A(0,2,0),C(2,0,0),D(1,2,0),E(0,0,2).
(Ⅰ)∵
=(-1,-2,2),
=(2,-2,0)
∴
•
=(-1)×2+(-2)×(-2)=2,
|
|=
=3,
|
|=
=2
∴cos<
,
>=
=
故异面直线DE与AC所成角的大小为arccos
;
(Ⅱ)假设线段CE上存在这样的点F,不妨设F(a,0,2-a)(0≤a≤2)
则
=(1,2,0),
=(a,0,2-a)

若设平面BDF的法向量为
=(x,y,z)
故有
,则
∴平面BDF的一个法向量为
=(2,-1,-
)
∵在平面ADE中,
=(-1,-2,2),
=(1,0,0)
同理可得平面ADE的一个法向量为
=(0,1,1)
由于平面BDF⊥平面ADE,则
⊥
,
即
•
=2×0+(-1)×1+(-
)×1=0
解得a=-2,由于点F在线段CE上,-2∉{a|0≤a≤2}
故在线段CE上不存在点F,使得平面BDF⊥平面ADE.
则AB,BC,BE两两垂直,
故可以B为原点建立如图所示空间直角坐标系B-xyz.

∵AB=BC=BE=2AD=2,
则B(0,0,0),A(0,2,0),C(2,0,0),D(1,2,0),E(0,0,2).
(Ⅰ)∵
| DE |
| AC |
∴
| DE |
| AC |
|
| DE |
| (-1)2+(-2)2+22 |
|
| AC |
| 22+(-2)2+02 |
| 2 |
∴cos<
| DE |
| AC |
| ||||
|
|
| ||
| 6 |
故异面直线DE与AC所成角的大小为arccos
| ||
| 6 |
(Ⅱ)假设线段CE上存在这样的点F,不妨设F(a,0,2-a)(0≤a≤2)
则
| BD |
| BF |

若设平面BDF的法向量为
| n |
故有
|
|
∴平面BDF的一个法向量为
| n |
| 2a |
| 2-a |
∵在平面ADE中,
| DE |
| AD |
同理可得平面ADE的一个法向量为
| m |
由于平面BDF⊥平面ADE,则
| m |
| n |
即
| m |
| n |
| 2a |
| 2-a |
解得a=-2,由于点F在线段CE上,-2∉{a|0≤a≤2}
故在线段CE上不存在点F,使得平面BDF⊥平面ADE.
点评:熟练掌握通过建立空间直角坐标系利用平面的法向量和直线的方向向量等知识证明线线、线面、面面垂直和求出异面直线所成的夹角的方法是解题的关键.

练习册系列答案
相关题目
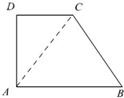
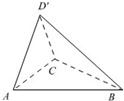
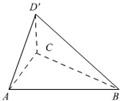
 (2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
(2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
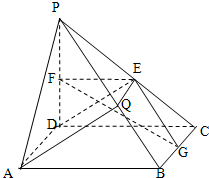
 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD= 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为