题目内容
(本小题满分12分)已知二次函数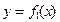 的
的 图象以原点为顶点且过点(1,1),反比例函数
图象以原点为顶点且过点(1,1),反比例函数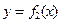 的图象与直线
的图象与直线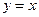 的两个交点间的距离为8,
的两个交点间的距离为8,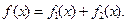
(1)求函数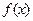 的表达式;
的表达式;
(2)证明:当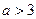 时,关于
时,关于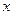 的方程
的方程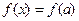 有三个实数解.
有三个实数解.
(1)由已知,设 ,由
,由
 ,得
,得 ,∴
,∴ ……2分
……2分
设 ,它的图象与直线
,它的图象与直线 的交点分别为
的交点分别为
由 ,得
,得
∴ 故
故 ……4分
……4分
(2)证明:由 ,得
,得
即  ……5分
……5分
在同一坐标系内作出 和
和 的大致图象如图,其中
的大致图象如图,其中 的图象是以坐标轴为渐近线,且位于第一、三象限的双曲线,
的图象是以坐标轴为渐近线,且位于第一、三象限的双曲线, 的图象是以
的图象是以 为顶点,开口向下的抛物线.
为顶点,开口向下的抛物线.
∴
 与
与 的图象在第三象限有一个交点,
的图象在第三象限有一个交点,
即 有一个负数解.…… 8分
有一个负数解.…… 8分
又∵
当
 时,
时,
∴当 时,在第一象限
时,在第一象限 的图象上存在一点
的图象上存在一点 在
在 图象的上方.
图象的上方.
∴ 与
与 的图象在第一象限有两个交点,[来源:Z.xx.k.Com]
的图象在第一象限有两个交点,[来源:Z.xx.k.Com]
即 有两个正数解.
有两个正数解.
∴方程 有三个实数解.…… 12分
有三个实数解.…… 12分
解析

练习册系列答案
相关题目
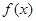 的最小值为1,且
的最小值为1,且 .
.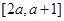 上不单调,求实数
上不单调,求实数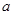 的取值范围;
的取值范围;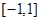 上,
上,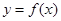 的图象恒在
的图象恒在 的图象上方,试确定实数
的图象上方,试确定实数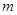 的
的 取值范围。
取值范围。
 上的函数
上的函数 的图象如右图所示
的图象如右图所示
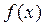 =ax2+(b-8)x-a-ab , 当x
=ax2+(b-8)x-a-ab , 当x (-∞,-3)
(-∞,-3) (2,+∞)时,
(2,+∞)时, 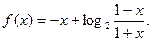
 的值;
的值; 在定义域内的单调性并给予证明.
在定义域内的单调性并给予证明.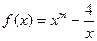 ,且
,且
 的值;
的值;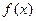 的奇偶性;
的奇偶性;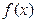 定义域为
定义域为 ,对于定义域内的任意x,y都有
,对于定义域内的任意x,y都有 ,且
,且 ,当
,当