题目内容
定义函数 ,若存在常数C,对任意的
,若存在常数C,对任意的 ,存在唯一的
,存在唯一的 ,使得
,使得 ,则称函数
,则称函数 在D上的几何平均数为C.已知
在D上的几何平均数为C.已知 ,则函数
,则函数 在
在 上的几何平均数为( )
上的几何平均数为( )
A. B.
B. C.
C. D.
D.
C
解析试题分析:根据关于函数f(x)在D上的几何平均数为C的定义,
且f(x)=x在区间[2,4]单调递增,所以 =2时,存在唯一的
=2时,存在唯一的 =4与之对应,
=4与之对应,
使C=  ,故选C.
,故选C.
考点:本题主要考查阅读理解能力。
点评:新定义问题,作为新定义问题,关键是理解“定义内容”,本题中通过“特举”,实现了利用特殊解决要不问题的愿望。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=x+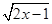 ( )
( )
A.有最小值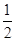 ,无最大值 ,无最大值 |
B.有最大值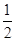 ,无最小值 ,无最小值 |
C.有最小值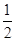 ,最大值2 ,最大值2 |
| D.无最大值,也无最小值 |
下列函数中,是奇函数且在区间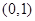 内单调递减的函数是( )
内单调递减的函数是( )
A.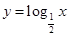 | B.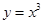 | C.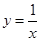 | D.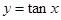 |
已知函数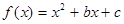 ,且
,且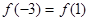 .则( )
.则( )
A.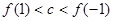 | B.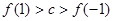 |
C.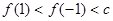 | D.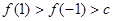 |
函数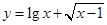 的定义域是( )
的定义域是( )
A.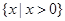 | B. | C.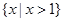 | D.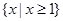 |
已知函数 ,
, ,且
,且 ,当
,当 时,
时, 是增函数,设
是增函数,设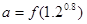 ,
,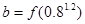 ,
, ,则
,则 、
、 、
、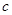 的大小顺序是( )。
的大小顺序是( )。
A. | B.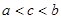 | C. | D. |
函数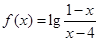 的定义域为( )
的定义域为( )
A.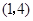 | B.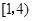 |
C.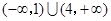 | D.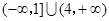 |
函数 的定义域是( )
的定义域是( )
A. | B. | C. | D.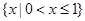 |
若函数 与函数
与函数 在区间
在区间 上都是减函数,则实数的取值范围为( )
上都是减函数,则实数的取值范围为( )
A. | B. | C. | D.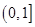 |