题目内容
如果自然数
的各位数字之和等于7，那么称为“吉祥数”.将所有“吉祥数”从小到大排成一列
若
则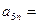
.
的各位数字之和等于7，那么称为“吉祥数”.将所有“吉祥数”从小到大排成一列若则 .
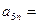52000∵方程
的非负整数解的个数为
.而使
的整数解个数为
.现取
，可知，
位“吉祥数”的个数为
∵2005是形如
的数中最小的一个“吉祥数”，且
对于四位“吉祥数”
，其个数为满足
的非负整数解个数，即
个。
∵2005是第1+7+28+28+1＝65个“吉祥数”，即
从而
又
而
∴从大到小最后六个五位“吉祥数”依次是：70000，61000,60100,60010,60001,52000.∴第325个“吉祥数”是52000，即
的非负整数解的个数为.而使的整数解个数为.现取，可知，位“吉祥数”的个数为∵2005是形如
的数中最小的一个“吉祥数”，且对于四位“吉祥数”，其个数为满足的非负整数解个数，即个。∵2005是第1+7+28+28+1＝65个“吉祥数”，即
从而又
而∴从大到小最后六个五位“吉祥数”依次是：70000，61000,60100,60010,60001,52000.∴第325个“吉祥数”是52000，即
练习册系列答案
相关题目
这六个数字组成的无重复数字的自然数，求：（1）有多少个含有
，
必须由大到小顺序排列的六位数？