题目内容
某大学共有A、B、C三个学生食堂,一个宿舍共有四名学生,在一段时间内,他们每天中午都在学生食堂用餐,且每个学生到这三个食堂中的任一食堂用餐的可能性都相等.用X表示这个宿舍每天中午在A食堂用餐的人数.根据这一时间段该宿舍学生的就餐情况解决下列问题:
(1)求每天中午每个学生食堂中至少有这个宿舍一名学生用餐的概率;
(2)求随机变量X的数学期望和方差.
解:(1)每天中午每个学生食堂中至少有这个宿舍一名学生用餐的情况有 种,
种,
四名学生到食堂用餐的情况共有34种,
∴每天中午每个学生食堂中至少有这个宿舍一名学生用餐的概率P= =
= .
.
(2)由题设知X的可能取值为0,1,2,3,4,
P(X=0)= =
=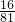 ,
,
P(X=1)= =
= ,
,
P(X=2)= =
=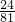 ,
,
P(X=3)= =
=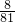 ,
,
P(X=4)= =
= ,
,
∴X的分布列为:
∴EX= +
+ =
= .
.
DX=(0- )2×
)2×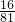 +(1-
+(1- )2×
)2× +(2-
+(2- )2×
)2×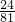 +(3-
+(3- )2×
)2×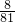 +(4-
+(4- )2×
)2× =
= .
.
分析:(1)每天中午每个学生食堂中至少有这个宿舍一名学生用餐的情况有 种,四名学生到食堂用餐的情况共有34种,由此能求出每天中午每个学生食堂中至少有这个宿舍一名学生用餐的概率.
种,四名学生到食堂用餐的情况共有34种,由此能求出每天中午每个学生食堂中至少有这个宿舍一名学生用餐的概率.
(2)由题设知X的可能取值为0,1,2,3,4,分别求出P(X=0),P(X=1),P(X=2),P(X=3),P(X=4),由此能求出X的数学期望和方差.
点评:本题考查概率的求法,考查离散型随机变量的数学期望和方差,是历年高考的必考题型,解题时要认真审题,仔细解答,注意合理地进行等价转化.
 种,
种,四名学生到食堂用餐的情况共有34种,
∴每天中午每个学生食堂中至少有这个宿舍一名学生用餐的概率P=
 =
= .
.(2)由题设知X的可能取值为0,1,2,3,4,
P(X=0)=
 =
=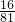 ,
,P(X=1)=
 =
= ,
,P(X=2)=
 =
=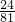 ,
,P(X=3)=
 =
=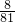 ,
,P(X=4)=
 =
= ,
,∴X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | 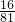 |  | 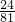 | 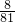 |  |
 +
+ =
= .
.DX=(0-
 )2×
)2×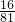 +(1-
+(1- )2×
)2× +(2-
+(2- )2×
)2×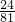 +(3-
+(3- )2×
)2×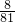 +(4-
+(4- )2×
)2× =
= .
.分析:(1)每天中午每个学生食堂中至少有这个宿舍一名学生用餐的情况有
 种,四名学生到食堂用餐的情况共有34种,由此能求出每天中午每个学生食堂中至少有这个宿舍一名学生用餐的概率.
种,四名学生到食堂用餐的情况共有34种,由此能求出每天中午每个学生食堂中至少有这个宿舍一名学生用餐的概率.(2)由题设知X的可能取值为0,1,2,3,4,分别求出P(X=0),P(X=1),P(X=2),P(X=3),P(X=4),由此能求出X的数学期望和方差.
点评:本题考查概率的求法,考查离散型随机变量的数学期望和方差,是历年高考的必考题型,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目

