��Ŀ����
(��)��ͼ,�غӱ�AB��һˮվP���ס�������ѧУ��ͬʹ��,��֪ѧУ����ӱ�1ǧ��,��ѧУ��ӱ�2ǧ��,���ס�����У���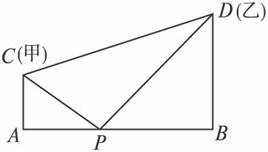
(1)��PA=x(x��0),�Խ�x��ʾ����ˮ��Ҫ��ˮ���ܳ�y�ĺ���;
(2)��ˮվP����ʲôλ��,����ˮ�ܵķ������?
(��)��һ��2��6��Ӳ�ְ尴ͼֽ��Ҫ����в���,���߲�ȥ��Ӱ����,��ʣ�ಿ�ְ�Ҫ�ӳ�һ���иǵij�����ˮ��(���Т���ۡ�����ֱܷ���ȫ�ȵľ���,�Ң�+��=��),��ˮ��ĸ�Ϊx��,�ݻ�Ϊy������.
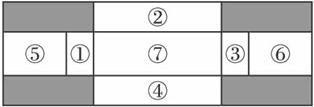
(1)��y����x�ĺ�����ϵʽ;
(2)������x�Ĵ�С,ʹ��ˮ��װ��ˮ���?
�𰸣�(��)��:(1)������,AB=3,CP=![]() ,DP=
,DP=![]() ��
��
��y=![]() (0��x��3).
(0��x��3).
(2)y��=![]() =0,
=0,
��![]() ,����ƽ��,��
,����ƽ��,��![]() ,
,
����,��x2+2x-3=0,����x=1.(x=-3��ȥ)����x=1ʱ����ˮ�ܵķ������.
(��)�⣺(1)��ˮ��ĸ�Ϊx(��),��ˮ�����ߵij������ֱ�Ϊ![]() =3-x(��)��
=3-x(��)��![]() =1-x(��).
=1-x(��).
��ˮ����ݻ�Ϊy=x(3-x)(1-x)=x3-4x2+3x(0��x��1).
(2)��y��=3x2-8x+3=0,��x=![]() ������y=x3-4x2+3x(0��x��1)��(0,
������y=x3-4x2+3x(0��x��1)��(0,![]() )�ϵ�������,��(
)�ϵ�������,��(![]() ,1)�ϵ����ݼ�.����x=
,1)�ϵ����ݼ�.����x=![]() ʱˮ����ݻ����.
ʱˮ����ݻ����.

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ���غӱ�AB��һˮվP���ס�������ѧУ��ͬʹ�ã���֪ѧУ����ӱ�1ǧ�ף�ѧУ����ӱ�2ǧ�ף����ס�����У���
��ͼ���غӱ�AB��һˮվP���ס�������ѧУ��ͬʹ�ã���֪ѧУ����ӱ�1ǧ�ף�ѧУ����ӱ�2ǧ�ף����ס�����У���
 ��ͼ���غӱ�AB��һˮվP���ס�������ѧУ��ͬʹ�ã���֪ѧУ����ӱ�1ǧ�ף�ѧУ����ӱ�2ǧ�ף����ס�����У���
��ͼ���غӱ�AB��һˮվP���ס�������ѧУ��ͬʹ�ã���֪ѧУ����ӱ�1ǧ�ף�ѧУ����ӱ�2ǧ�ף����ס�����У��� ǧ�ף������У������ͬһ����۵�ˮ����ˮ��
ǧ�ף������У������ͬһ����۵�ˮ����ˮ�� ǧ�ף������У������ͬһ����۵�ˮ����ˮ��
ǧ�ף������У������ͬһ����۵�ˮ����ˮ��