题目内容
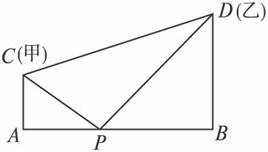
如图，沿河边AB建一水站P供甲、乙两个学校共同使用，已知学校甲离河边1千米，学校乙离河边2千米，而甲、乙两校相距| 10 |
（1）设PA=x（x＞0），试将x表示成送水需要的水管总长y的函数；
（2）问水站P建在什么位置，购买水管的费用最低？
分析：（1）先分别求出AB、CP、DP的长，然后根据送水需要的水管总长等于AB+CP+DP建立关系式，注意定义域；
（2）求出函数的导函数，然后令导数等于0，求出极值点，从而求出水站P建在什么位置，购买水管的费用最低．
（2）求出函数的导函数，然后令导数等于0，求出极值点，从而求出水站P建在什么位置，购买水管的费用最低．
解答：
解：（1）由题意：AB=3，CP=
，DP=
故：y=
+
(0＜x＜3)
（2）y′=
+
=0
即：
=-
两边平方：
化简：x2+2x-3=0所以x=1，（x=-3舍去）
答：x=1时，也就是水站建在离A点1千米处购买水管的费用最低．
解：（1）由题意：AB=3，CP=| x2+1 |
| (3-x)2+4 |
故：y=
| x2+1 |
| (3-x)2+4 |
（2）y′=
| x | ||
|
| x-3 | ||
|
即：
| x | ||
|
| x-3 | ||
|
化简：x2+2x-3=0所以x=1，（x=-3舍去）
答：x=1时，也就是水站建在离A点1千米处购买水管的费用最低．
点评：本题主要考查了函数模型的选择与应用，以及利用导数求闭区间上函数的最值，属于中档题．
练习册系列答案
相关题目
千米,如果两校决定用同一种造价的水管送水.
