题目内容

11．函数f（x）=$\left\{\begin{array}{l}{{2}^{-x}（x≤0）}\\{Asin\frac{πx}{4}（x＞0）}\end{array}\right.$（A＞0），则下列结论正确的是（　　）
A．?常数T＞0，使f（x+T）=f（x）
B．?A，图象上不存在关于原点中心对称的点
C．?A，f（x）存在最大值与最小值
D．?A，使f（x）在[a，b]上的值域也是[a，b]

分析 作函数f（x）=$\left\{\begin{array}{l}{{2}^{-x}（x≤0）}\\{Asin\frac{πx}{4}（x＞0）}\end{array}\right.$（A＞0）的图象，结合图象对选项A，B，C分析即可．

解答 解：作函数f（x）=$\left\{\begin{array}{l}{{2}^{-x}（x≤0）}\\{Asin\frac{πx}{4}（x＞0）}\end{array}\right.$（A＞0）的图象如下，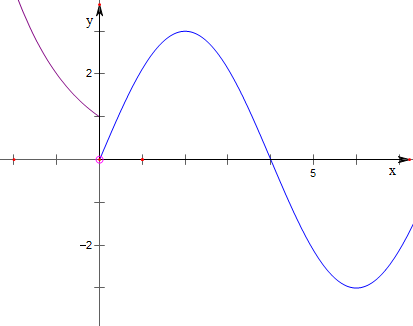

结合图象可知，不存在常数T＞0，使f（x+T）=f（x），故A不正确；
易知点（-6，64）在函数f（x）的图象上，
故当A=64时，（6，-64）也在函数f（x）的图象上，故B不正确；
∵x→∞时，f（x）→+∞；故f（x）不存在最大值；故C不正确；
故选：D．

点评 本题考查了分段函数的综合应用．

练习册系列答案
相关题目
15．已知M=ab+1，N=a+b，Q=$\frac{1}{2|a|}$+$\frac{|a|}{b}$，a，b∈R．
（1）证明：当a＞1，b＞1时，M＞N；
（2）若a+b=2，b＞0，求当Q取最小值时a的值．
16．在△ABC中，角A、B、c所对的边分别为a、b、c．又∠A=60°，sinB：sincC=2：3，AB边上的高为3$\sqrt{3}$，求a，b，c．
13．一个星级旅馆有150个标准房，经过一段时间的经营，得到一些定价和住房率的数据如下：
房价（元）住房率（%）
16055
14065
12075
10085
欲使每天的营业额最高，应如何定价？
6．在正方体ABCD-A′B′C′D′中，点M为面A′B′C′D′的任意一点，那么∠MAA′＜30°的概率为$\frac{π}{12}$．
16．设函数fn（x）=xn+kx+m（n∈N+，k，m∈R）
（1）设n≥2，k=1，m=-1，证明：fn（x）在区间（$\frac{1}{2}$，1）内存在唯一的零点
（2）设n=2，k=-2，集合D={f（x）|f（x）在定义域内存在区间[a，b]，使得f（x）在[a，b]上的值域也为[a，b]，是否存在实数m，当a+b≤2时，使得函数fn（x）∈D，若存在，求出m的范围，若不存在，说明理由．
3．求函数y=x3-2x2-x+2的零点，并画出它的图象．
20．已知tan（$\frac{π}{4}$+α）=3，且α为锐角．
（1）求tanα的值；
（2）求sin（α+$\frac{π}{6}$）的值．
1．点p在曲线y=x3-x+3上移动，过点p的切线方程的倾斜角的取值范围有是（　　）
A．[0，π）B．[0，$\frac{π}{2}$）∪[$\frac{3}{4}$π，π）C．[0，$\frac{π}{2}$]∪（$\frac{π}{2}$，$\frac{3}{4}$π]D．[0，$\frac{π}{4}$]∪[$\frac{3}{4}$π，π）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网