题目内容
已知复平面内平行四边形ABCD,A点对应的复数为2+i,向量 对应的复数为1+2i,向量
对应的复数为1+2i,向量 对应的复数为3-i.
对应的复数为3-i.
(1)求点C,D对应的复数;
(2)求平行四边形ABCD的面积.
解:(1)∵向量 对应的复数为1+2i,向量
对应的复数为1+2i,向量 对应的复数为3-i,
对应的复数为3-i,
∴向量 对应的复数为(1+2i)-(3-i)=2-3i,
对应的复数为(1+2i)-(3-i)=2-3i,
又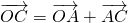 ,
,
∴点C对应的复数为(2+i)+(2-3i)=4-2i.
又 =(1+2i)+(3-i)=4+i,
=(1+2i)+(3-i)=4+i,
 =2+i-(1+2i)=1-i,
=2+i-(1+2i)=1-i,
∴ =1-i+(4+i),∴点D对应的复数为5.
=1-i+(4+i),∴点D对应的复数为5.
(2)∵
∴ ,
,
∴sinB= ,
,
∴S= =
= .
.
∴平行四边形ABCD的面积为7.
分析:(1)表示向量 对应的复数,用
对应的复数,用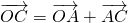 求点C对应的复数;
求点C对应的复数; 求出D对应的复数;
求出D对应的复数;
(2)由 求出cosB,再求sinB,利用
求出cosB,再求sinB,利用 求平行四边形ABCD的面积.
求平行四边形ABCD的面积.
点评:本题考查复数的基本概念,平面向量数量积的运算,考查计算能力,是基础题.
 对应的复数为1+2i,向量
对应的复数为1+2i,向量 对应的复数为3-i,
对应的复数为3-i,∴向量
 对应的复数为(1+2i)-(3-i)=2-3i,
对应的复数为(1+2i)-(3-i)=2-3i,又
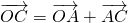 ,
,∴点C对应的复数为(2+i)+(2-3i)=4-2i.
又
 =(1+2i)+(3-i)=4+i,
=(1+2i)+(3-i)=4+i, =2+i-(1+2i)=1-i,
=2+i-(1+2i)=1-i,∴
 =1-i+(4+i),∴点D对应的复数为5.
=1-i+(4+i),∴点D对应的复数为5.(2)∵

∴
 ,
,∴sinB=
 ,
,∴S=
 =
= .
.∴平行四边形ABCD的面积为7.
分析:(1)表示向量
 对应的复数,用
对应的复数,用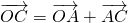 求点C对应的复数;
求点C对应的复数; 求出D对应的复数;
求出D对应的复数;(2)由
 求出cosB,再求sinB,利用
求出cosB,再求sinB,利用 求平行四边形ABCD的面积.
求平行四边形ABCD的面积.点评:本题考查复数的基本概念,平面向量数量积的运算,考查计算能力,是基础题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 对应的复数为1+2i,向量
对应的复数为1+2i,向量 对应的复数为3-i.
对应的复数为3-i.