题目内容
已知函数 图象上一点
图象上一点 处的切线方程为
处的切线方程为 .
.
(1)求 的值;
的值;
(2)若方程 在
在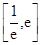 内有两个不等实根,求
内有两个不等实根,求 的取值范围(其中
的取值范围(其中 为自然对数的底数);(3)令
为自然对数的底数);(3)令 ,若
,若 的图象与
的图象与 轴交于
轴交于 (其中
(其中 ),
), 的中点为
的中点为 ,求证:
,求证: 在
在 处的导数
处的导数
(1)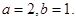 ;(2)
;(2)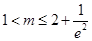 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)属于简单题,利用函数在 的导数值为斜率求解;(2)转化为函数
的导数值为斜率求解;(2)转化为函数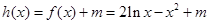 与
与 轴有2个交点,进来转化为求函数的最大值与最小值问题,利用导数判函数的单调性满足
轴有2个交点,进来转化为求函数的最大值与最小值问题,利用导数判函数的单调性满足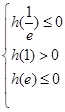 即可;(3)利用反证法求解,假设
即可;(3)利用反证法求解,假设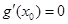 成立,由条件满足
成立,由条件满足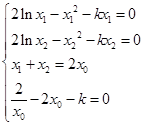 ,利用第1、2个条件求解
,利用第1、2个条件求解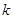 值,结合第4个条件得到
值,结合第4个条件得到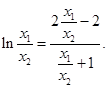 ,再利用函数的单调性充分证明假设错误,进而得证
,再利用函数的单调性充分证明假设错误,进而得证 在
在 处的导数
处的导数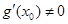 .
.
试题解析:(1)
 且
且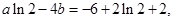
解得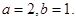 3分
3分
(2)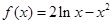 ,令
,令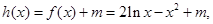
则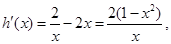
令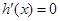 ,得
,得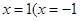 舍去).
舍去).
当 时,
时,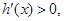
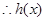 是增函数;
是增函数;
当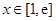 时,
时,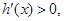
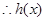 是减函数; 5分
是减函数; 5分
于是方程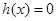 在
在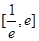 内有两个不等实根的充要条件是:
内有两个不等实根的充要条件是: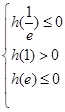 .
.
即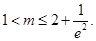 9分
9分
(3)由题意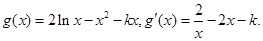
假设结论成立,则有: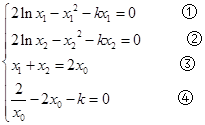 11分
11分
①-②,得
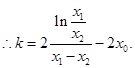
由④得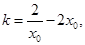
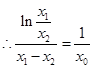
即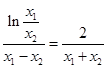 ,即
,即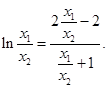 ⑤ 13分
⑤ 13分
令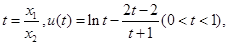
则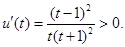
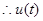 在(0,1)增函数,
在(0,1)增函数,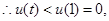
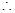 ⑤式不成立,与假设矛盾.
⑤式不成立,与假设矛盾.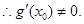 14分
14分
考点:1.利用导数判函数的单调性;2.函数的最值求解;3.反证法思想.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 的解集为M,求当x∈M时函数
的解集为M,求当x∈M时函数 的最大、最小值.
的最大、最小值.
 的定义域是
的定义域是 ,求实数
,求实数 的取值范围及
的取值范围及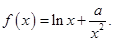
 辟为水果园,其中
辟为水果园,其中 ,
, 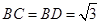 ,
, .若经过
.若经过 上一点
上一点 和
和 上一点
上一点 铺设一条道路
铺设一条道路 ,且
,且 .
.
 的关系式;
的关系式; 的位置在哪里?
的位置在哪里?
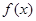 的值域;
的值域; 时,函数
时,函数 ,求
,求 的值和函数
的值和函数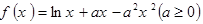 .
.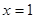 是函数
是函数 的极值点,求
的极值点,求 的值;
的值;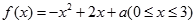 的最大值为
的最大值为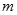 ,最小值为
,最小值为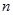 ,其中
,其中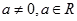 .
.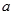 表示);
表示);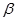 的顶点与平面直角坐标系
的顶点与平面直角坐标系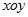 中的原点
中的原点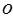 重合,始边与
重合,始边与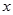 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点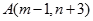 .求
.求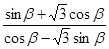 的值.
的值.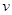 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度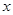 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当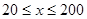 时,车流速度
时,车流速度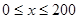 时,求函数
时,求函数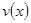 的表达式;
的表达式; 可以达到最大,并求出最大值.(精确到1辆/小时).
可以达到最大,并求出最大值.(精确到1辆/小时).