题目内容
已知函数
(1)求函数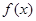 的值域;
的值域;
(2)若 时,函数
时,函数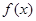 的最小值为
的最小值为 ,求
,求 的值和函数
的值和函数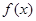 的最大值。
的最大值。
(1)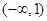 ;(2)
;(2)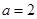 或
或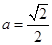 ,当
,当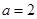 时f(x)的最大值为
时f(x)的最大值为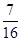 ;当
;当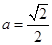 时f(x)的最大值为
时f(x)的最大值为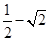 。
。
解析试题分析:(1)本题通过换元转化为二次函数最值问题,再利用单调性求最值,从而得到函数值域;(2)某区间上的二次函数最值问题,要进行配方,确定对称轴,弄清单调性,才能求解.如果对称轴不确定,要进行分类讨论来解决.
试题解析:设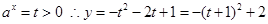 2分
2分
(1)
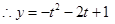 在
在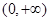 上是减函数
上是减函数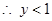 , 所以值域为
, 所以值域为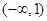 . 6分
. 6分
(2)①当 时,
时,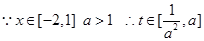 由
由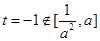
所以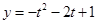 在
在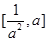 上是减函数,
上是减函数,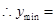
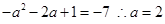 或
或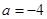 (不合题意舍去) 8分
(不合题意舍去) 8分
当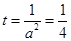 时
时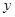 有最大值,
有最大值,
即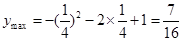 10分
10分
②当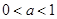 时,
时,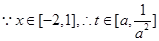 ,
,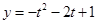 在上
在上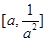 是减函数,
是减函数,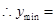
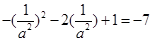 ,
,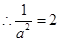 或
或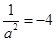 (不合题意舍去)
(不合题意舍去)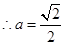 或
或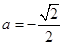 (舍去) 12分
(舍去) 12分
当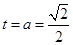 时y有最大值,即
时y有最大值,即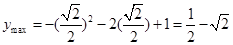
综上,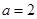 或
或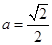 ,当
,当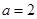 时f(x)的最大值为
时f(x)的最大值为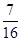 ;
;
当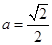 时f(x)的最大值为
时f(x)的最大值为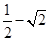 。 14分
。 14分
考点:1、指数函数最值;2、分类讨论思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (其中
(其中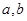 为常数且
为常数且  )的图象经过点
)的图象经过点 .
. 的解析式;
的解析式; 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围. 的解集为M.
的解集为M. ,求实数
,求实数 的取值范围;
的取值范围; ,求实数
,求实数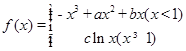 的图像在点
的图像在点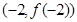 处的切线方程为
处的切线方程为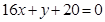 .
.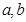 的值;
的值; 在区间
在区间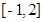 上的最大值;
上的最大值;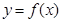 上存在两点
上存在两点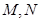 使得
使得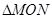 是以坐标原点
是以坐标原点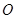 为直角顶点的直角三角形,且斜边
为直角顶点的直角三角形,且斜边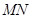 的中点在
的中点在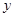 轴上,求实数
轴上,求实数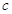 的取值范围.
的取值范围. 图象上一点
图象上一点 处的切线方程为
处的切线方程为 .
. 的值;
的值; 在
在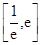 内有两个不等实根,求
内有两个不等实根,求 的取值范围(其中
的取值范围(其中 为自然对数的底数);(3)令
为自然对数的底数);(3)令 ,若
,若 的图象与
的图象与 轴交于
轴交于 (其中
(其中 ),
), 的中点为
的中点为 ,求证:
,求证: 处的导数
处的导数
 .
.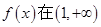 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;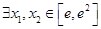 ,使
,使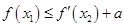 成立,求实数a的取值范围.
成立,求实数a的取值范围.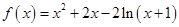 .
. 的单调区间;
的单调区间; 时,是否存在整数
时,是否存在整数 ,使不等式
,使不等式 恒成立?若存在,求整数
恒成立?若存在,求整数 的方程
的方程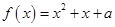 在
在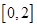 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数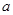 的取值范围.
的取值范围.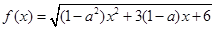 .若
.若 的定义域为
的定义域为 ,求实数
,求实数 的取值范围.
的取值范围. 千件,需另投入成本为
千件,需另投入成本为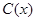 ,当年产量不足80千件时,
,当年产量不足80千件时, (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完. (万元)关于年产量
(万元)关于年产量