题目内容
已知函数
(1)解不等式f(x)>1;
(2)求函数y=f(x)的最大值.
解:(1)当x 时,f(x)>1,即
时,f(x)>1,即 ,∴x
,∴x ,此时无解.
,此时无解.
当x 时,f(x)>1,可得
时,f(x)>1,可得 解得x
解得x ,所以
,所以 .
.
当x≥4时,f(x)>1,可得 ,解得x
,解得x ,所以
,所以 ,
,
综上不等式的交集为: .
.
(2)f(x)=
函数在x≤4时是增函数,x≥4时是减函数,函数y=f(x)的最大值为: .
.
分析:(1)通过对x的范围分类讨论,化简不等式分别求出解集,然后求出并集即可.
(2)通过判断函数的单调性,直接求出函数的最大值,即可.
点评:本题考查绝对值不等式的解法,分类讨论思想的应用,函数的单调性的应用,考查计算能力.
 时,f(x)>1,即
时,f(x)>1,即 ,∴x
,∴x ,此时无解.
,此时无解.当x
 时,f(x)>1,可得
时,f(x)>1,可得 解得x
解得x ,所以
,所以 .
.当x≥4时,f(x)>1,可得
 ,解得x
,解得x ,所以
,所以 ,
,综上不等式的交集为:
 .
.(2)f(x)=

函数在x≤4时是增函数,x≥4时是减函数,函数y=f(x)的最大值为:
 .
.分析:(1)通过对x的范围分类讨论,化简不等式分别求出解集,然后求出并集即可.
(2)通过判断函数的单调性,直接求出函数的最大值,即可.
点评:本题考查绝对值不等式的解法,分类讨论思想的应用,函数的单调性的应用,考查计算能力.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
 (a,b为不等零的实数),满足f(2)=1且f(x)=x有唯一解,试求函数y=f(x)的解析式.
(a,b为不等零的实数),满足f(2)=1且f(x)=x有唯一解,试求函数y=f(x)的解析式.
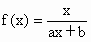 (a,b为不等零的实数),满足f(2)=1且f(x)=x有唯一解,试求函数y=f(x)的解析式.
(a,b为不等零的实数),满足f(2)=1且f(x)=x有唯一解,试求函数y=f(x)的解析式.
 的解集
的解集 有两个不等的实数根,求
有两个不等的实数根,求 的取值范围
的取值范围
 的解集
的解集 有两个不等的实数根,求
有两个不等的实数根,求 的取值范围
的取值范围