题目内容
设函数 .
.(1)当a=2时,求f(x)的最大值;
(2)令
 (0<x≤3),以其图象上任意一点P(x,y)为切点的切线的斜率
(0<x≤3),以其图象上任意一点P(x,y)为切点的切线的斜率 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;(3)当a=0时,方程mf(x)=x2有唯一实数解,求正数m的值.
【答案】分析:(1)把a=2代入函数 ,对f(x)进行求导,求出其极值,根据导数来求最值;
,对f(x)进行求导,求出其极值,根据导数来求最值;
(2)对F(x)进行求导,求过点P(x,y)的切线,求出k用x0的表达出来,再根据斜率 恒成立,从而求出a的范围;
恒成立,从而求出a的范围;
(3)当a=0时,方程mf(x)=x2即x2-mx-mlnx=0,令g(x)=x2-mx-mlnx,对其进行求导,利用导数来画出函数的草图,从而来求解;
解答:解(1)a=2时,f(x)=lnx+x-x2, …(1分),
…(1分),
解f′(x)=0得x=1或 (舍去)…(2分),
(舍去)…(2分),
当x∈(0,1)时,f′(x)>0,f(x)单调增加,
当x∈(1,+∞)时,f′(x)<0,f(x)单调减少…(3分),
所以f(x)的最大值为f(1)=0…(4分)
(2) (0<x≤3),
(0<x≤3), (0<x≤3)…(6分)
(0<x≤3)…(6分)
由 恒成立得
恒成立得 恒成立…(7分)
恒成立…(7分)
因为 ,等号当且仅当x=1时成立…(8分),
,等号当且仅当x=1时成立…(8分),
所以 …(9分)
…(9分)
(3)a=0时,方程mf(x)=x2即x2-mx-mlnx=0,
设g(x)=x2-mx-mlnx,
解 …(10分),得
…(10分),得 (<0舍去),
(<0舍去), ,
,
类似(1)的讨论知,g(x)在x∈(0,x2)单调增加,
在x∈(x2,+∞)单调减少,最大值为g(x2)…(11分),
因为mf(x)=x2有唯一实数解,g(x)有唯一零点,所以g(x2)=0…(12分),
由 得x2+2lnx2-1=0,
得x2+2lnx2-1=0,
因为h(x)=x+lnx-1单调递增,且h(1)=0,
所以x2=1…(13分),
从而m=1…(14分).
点评:此题考查利用导数来研究函数的切线,最值和函数的单调性,是高考必考的一类题,此题是一道中档题.
 ,对f(x)进行求导,求出其极值,根据导数来求最值;
,对f(x)进行求导,求出其极值,根据导数来求最值;(2)对F(x)进行求导,求过点P(x,y)的切线,求出k用x0的表达出来,再根据斜率
 恒成立,从而求出a的范围;
恒成立,从而求出a的范围;(3)当a=0时,方程mf(x)=x2即x2-mx-mlnx=0,令g(x)=x2-mx-mlnx,对其进行求导,利用导数来画出函数的草图,从而来求解;
解答:解(1)a=2时,f(x)=lnx+x-x2,
 …(1分),
…(1分),解f′(x)=0得x=1或
 (舍去)…(2分),
(舍去)…(2分),当x∈(0,1)时,f′(x)>0,f(x)单调增加,
当x∈(1,+∞)时,f′(x)<0,f(x)单调减少…(3分),
所以f(x)的最大值为f(1)=0…(4分)
(2)
 (0<x≤3),
(0<x≤3), (0<x≤3)…(6分)
(0<x≤3)…(6分)由
 恒成立得
恒成立得 恒成立…(7分)
恒成立…(7分)因为
 ,等号当且仅当x=1时成立…(8分),
,等号当且仅当x=1时成立…(8分),所以
 …(9分)
…(9分)(3)a=0时,方程mf(x)=x2即x2-mx-mlnx=0,
设g(x)=x2-mx-mlnx,
解
 …(10分),得
…(10分),得 (<0舍去),
(<0舍去), ,
,类似(1)的讨论知,g(x)在x∈(0,x2)单调增加,
在x∈(x2,+∞)单调减少,最大值为g(x2)…(11分),
因为mf(x)=x2有唯一实数解,g(x)有唯一零点,所以g(x2)=0…(12分),
由
 得x2+2lnx2-1=0,
得x2+2lnx2-1=0,因为h(x)=x+lnx-1单调递增,且h(1)=0,
所以x2=1…(13分),
从而m=1…(14分).
点评:此题考查利用导数来研究函数的切线,最值和函数的单调性,是高考必考的一类题,此题是一道中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 。
。 的极值;
的极值; 2时,讨论函数
2时,讨论函数 成立,求
成立,求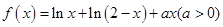 。
。 的单调区间。
的单调区间。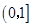 上的最大值为
上的最大值为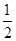 ,求a的值。
,求a的值。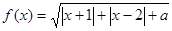 。
。 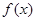 的定义域。
的定义域。 。
。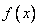 的单调区间。
的单调区间。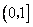 上的最大值为
上的最大值为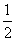 ,求a的值。
,求a的值。