Question

已知棱长为1的正方体ABCD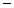A1B1C1D1中, P,Q是面对角线A1C1上的两个不同动点.

①存在P,Q两点,使BP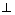DQ;

②存在P,Q两点,使BP,DQ与直线B1C都成450的角;

③若|PQ|=1,则四面体BDPQ的体积一定是定值;

④若|PQ|=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为定值.

以上命题为真命题的个数是( )

A．1 B．2 　　　　C．3 D．4

 

Answer 1

【答案】

C

【解析】

试题分析：①存在P,Q两点,使BPDQ是正确的，因为当P为,Q为时BPDQ；②存在P,Q两点,使BP,DQ与直线B1C都成450的角是错误的，因为BP与直线B1C所成的角最小角为；③若|PQ|=1,则四面体BDPQ的体积一定是定值是正确的，设与的交点为，则平面，平面将四面体BDPQ分成两个棱锥，高的和为，故体积不变；④若|PQ|=1, ,则四面体BDPQ在该正方体六个面上的正投影的面积的和为定值是正确的，当P,Q在面对角线A1C1上移动时，在各个面上的正投影的面积不变，故它的正投影的面积的和为定值．

考点：正方体的综合问题．