题目内容
如图所示,已知过点(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A、B两点,AD、BC垂直于直线y=-8,垂足分别为D、C,求矩形ABCD面积的最大值.

答案:
解析:
解析:
|
解析:设切点为(x0,y0),则y0=-a ∵ ∴|AB|=2a,|BC|=8-a3,∴矩形ABCD的面积S=16a-2a4,∴ ∴当0<a< 当a= 当 |

练习册系列答案
相关题目
 如图所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
如图所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
 为圆心的圆与直线
为圆心的圆与直线 相切.过点
相切.过点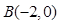 的动直线
的动直线 与圆
与圆 相交于
相交于 ,
, 两点,
两点, 是
是 的中点,直线
的中点,直线 相交于点
相交于点 .
.
 时,求直线
时,求直线 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由. 为圆心的圆与直线
为圆心的圆与直线 相切,过点
相切,过点 的动直线
的动直线 与圆
与圆 相交于
相交于 两点,
两点,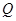 是
是 的中点,直线
的中点,直线 相交于点
相交于点 .
.
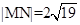 时,求直线
时,求直线 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.