题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解析:直线l过点(0,1),且方向向量a=(1,k),∴直线l的方程为y=kx+1.将其代入⊙C方程,得(1+k2)x2-4(1+k)x+7=0( 由△=[-4(1+k)]2-4·(1+k2)·7>0,得 |
(2) |
由平面几何知识,若过A的圆C的一条切线为AT(T为切点),则 |
(3) |
设M(x1,y1)、N(x2,y2),则由( ∴ =x1x2+(kx1+1)(kx2+1) =(1+k2)x1x2+k(x1+x2)+1 =(1+k2)· = ∴ 点评:本题根据向量数量积的坐标表示将题目中的 |

练习册系列答案
相关题目


 如图所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
如图所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
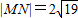 时,求直线l的方程.
时,求直线l的方程.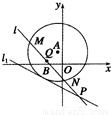
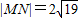 时,求直线l的方程.
时,求直线l的方程.