题目内容
已知集合A={x|-2＜x≤5}，B={x|m+1≤x≤2m-1}且A⊆B，求实数m的取值范围．
解：集合A={x|-2＜x≤5}，B={x|m+1≤x≤2m-1}，
由A⊆B得：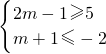
，
解得：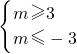
，
集合A是集合B的子集，说明集合B不能为空集，所以2m-1≥m+1，解得m≥2
所以实数m的取值范围∅．
分析：化简后的基础上，借助于子集概念得到两集合端点值的关系，求解不等式得到m的范围．
点评：本题考查了集合的包含关系判断及应用，考查了不等式的解法，是基础题．
由A⊆B得：
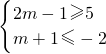，解得：
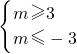，集合A是集合B的子集，说明集合B不能为空集，所以2m-1≥m+1，解得m≥2
所以实数m的取值范围∅．
分析：化简后的基础上，借助于子集概念得到两集合端点值的关系，求解不等式得到m的范围．
点评：本题考查了集合的包含关系判断及应用，考查了不等式的解法，是基础题．
练习册系列答案
相关题目