题目内容
函数y=sin（
-2x）的单调增区间是
- A.
，
]（k∈z） - B.
，
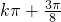]（k∈z） - C.
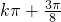，]（k∈z） - D.
，
]（k∈z）
D
分析：求三角函数的单调区间，一般要将自变量的系数变为正数，再由三角函数的单调性得出自变量所满足的不等式，求解即可得出所要的单调递增区间．
解答：y=sin（-2x）=-sin（2x-）
令
，k∈Z解得
，k∈Z
函数的递增区间是，]（k∈Z）
故选D．
点评：本题考查正弦函数的单调性，求解本题的关键有二，一是将自变量的系数为为正，二是根据正弦函数的单调性得出相位满足的取值范围，解题时不要忘记引入的参数的取值范围即k∈Z．
分析：求三角函数的单调区间，一般要将自变量的系数变为正数，再由三角函数的单调性得出自变量所满足的不等式，求解即可得出所要的单调递增区间．
解答：y=sin（
-2x）=-sin（2x-）令
，k∈Z解得，k∈Z函数的递增区间是
，]（k∈Z）故选D．
点评：本题考查正弦函数的单调性，求解本题的关键有二，一是将自变量的系数为为正，二是根据正弦函数的单调性得出相位满足的取值范围，解题时不要忘记引入的参数的取值范围即k∈Z．
练习册系列答案
阅读快车系列答案
相关题目