题目内容
(本题满分12分)
已知函数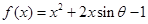 ,
,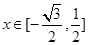
(1)当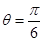 时,求
时,求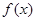 的最大值和最小值
的最大值和最小值
(2)若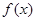 在
在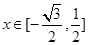 上是单调函数,且
上是单调函数,且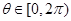 ,求
,求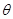 的取值范围
的取值范围
已知函数
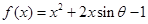 ,
,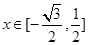
(1)当
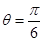 时,求
时,求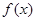 的最大值和最小值
的最大值和最小值(2)若
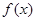 在
在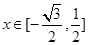 上是单调函数,且
上是单调函数,且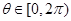 ,求
,求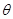 的取值范围
的取值范围(1)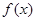 有最小值
有最小值 ,有最大值
,有最大值 (2)
(2)
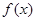 有最小值
有最小值 ,有最大值
,有最大值 (2)
(2)
试题分析:(1)当
 时,
时,
 在
在 上单调递减,在
上单调递减,在 上单调递增
上单调递增 当
当 时,函数
时,函数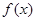 有最小值
有最小值
当
 时,函数
时,函数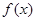 有最小值
有最小值 …………………………………(6分)
…………………………………(6分)(2)要使
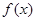 在
在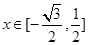 上是单调函数,则
上是单调函数,则 或
或
即
 或
或 ,又
,又
解得:
 …………………………………(12分)
…………………………………(12分)点评:二次函数求最值结合图像对称轴与定义域,单调区间以对称轴为区间边界

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
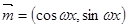 ,
,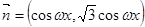 ,设函数
,设函数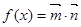 .
. 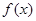 的零点组成公差为
的零点组成公差为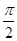 的等差数列,求函数
的等差数列,求函数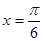 ,(
,(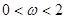 ),求函数
),求函数 的图象(部分)如图所示,则
的图象(部分)如图所示,则 和
和 的取值是
的取值是 




 中,
中, ,则
,则 ( )
( )



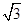 cosx (xÎR).
cosx (xÎR).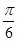 )=
)=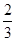 ,求cos2A的值.
,求cos2A的值.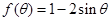 ,
,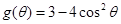 . 记
. 记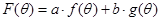 (其中
(其中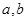 都为常数,且
都为常数,且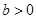 ).
). 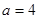 ,
,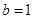 ,求
,求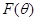 的最大值及此时的
的最大值及此时的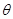 值;
值;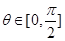 ,①证明:
,①证明: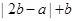 ;②证明:
;②证明: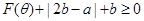 .
.
 的最小正周期及单调递减区间;
的最小正周期及单调递减区间; 时,函数
时,函数 ,求不等式
,求不等式 的解集.
的解集.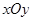 中,以
中,以 轴为始边做两个锐角
轴为始边做两个锐角 ,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为
,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为 .
. 的值; (2)求
的值; (2)求 的值.
的值.

 =
= ,在函数
,在函数
 +
+ 的图象中,对称中心到对称轴的最小距离为
的图象中,对称中心到对称轴的最小距离为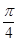 ,且当
,且当 时,
时,  的最大值为
的最大值为 .
.