题目内容
【题目】已知函数![]() ,
, ![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)当![]() 时,若直线
时,若直线![]() :
: ![]() 与曲线
与曲线![]() 没有公共点,求
没有公共点,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,函数
时,函数![]() 无极值;当
无极值;当![]() 时,
时, ![]() 有极小值为
有极小值为![]() ,无极大值.
,无极大值.
(2)![]() .
.
【解析】试题分析:(1)求得![]() ,可分
,可分![]() 和
和![]() 两种情况分类讨论,得出函数的单调性,即可求得函数的极值;
两种情况分类讨论,得出函数的单调性,即可求得函数的极值;
(2)当![]() 时,把直线
时,把直线![]() :
: ![]() 与曲线
与曲线![]() 没有公共点,等价于关于
没有公共点,等价于关于![]() 的方程
的方程![]() 在
在![]() 上没有实数解,即关于
上没有实数解,即关于![]() 的方程
的方程![]() 在
在![]() 上没有实数解,即
上没有实数解,即![]() 在
在![]() 上没有实数解,令
上没有实数解,令![]() ,利用导数求得函数
,利用导数求得函数![]() 的单调性与极值,即可求解实数
的单调性与极值,即可求解实数![]() 的取值范围.
的取值范围.
试题解析:
(1)![]() 定义域为
定义域为![]() ,
, ![]() .
.
①当![]() 时,
时, ![]() ,
, ![]() 为
为![]() 上的增函数,所以函数
上的增函数,所以函数![]() 无极值.
无极值.
②当![]() 时,令
时,令![]() ,解得
,解得![]() .
.
当![]() ,
, ![]() ,
, ![]() 在
在![]() 上单调递减;
上单调递减;
当![]() ,
, ![]() ,
, ![]() 在
在![]() 上单调递增.
上单调递增.
故![]() 在
在![]() 处取得极小值,且极小值为
处取得极小值,且极小值为![]() ,无极小值.
,无极小值.
综上,当![]() 时,函数
时,函数![]() 无极值;
无极值;
当![]() 时,
时, ![]() 有极小值为
有极小值为![]() ,无极大值.
,无极大值.
(2)当![]() 时,
时, ![]() ,
,
直线![]() :
: ![]() 与曲线
与曲线![]() 没有公共点,等价于关于
没有公共点,等价于关于![]() 的方程
的方程![]()
在![]() 上没有实数解,即关于
上没有实数解,即关于![]() 的方程
的方程![]() 在
在![]() 上没有实数解,
上没有实数解,
即![]() 在
在![]() 上没有实数解.
上没有实数解.
令![]() ,则有
,则有![]() .令
.令![]() ,解得
,解得![]() ,
,
当![]() 变化时,
变化时, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
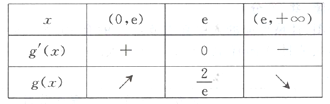
且当![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() 的最大值为
的最大值为![]() ;当
;当![]() 时,
时, ![]() ,
,
从而![]() 的取值范围为
的取值范围为![]() .
.
所以当![]() 时,方程
时,方程![]() 无实数解,
无实数解,
解得![]() 的取值范围是
的取值范围是![]() .
.

【题目】在一次恶劣气候的飞行航程中调查男女乘客在飞机上晕机的情况,共调查了89位乘客,其中男乘客有24人晕机,31人不晕机;女乘客有8人晕机,26人不晕机
(1)根据此材料数据完成如下的2×2列联表;
晕机 | 不晕机 | 总计 | |
男人 | |||
女人 | |||
总计 |
(2)根据列联表,利用下列公式和数据分析,你是否有90%的把握认为在本次飞机飞行中晕机与性别有关?
(3)其中8名晕机的女乘客中有5名是常坐飞机的乘客,另外3名是不常坐飞机的,从这8名乘客中任选3名,这3名乘客不都是常坐飞机的概率是多少?
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式: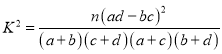 ,其中
,其中![]()
