题目内容
曲线C上任一点到点F1(-4,0),F2(4,0)的距离之和为12.曲线C的左顶点为A,点P在曲线C上,且PA⊥PF2.(Ⅰ)求曲线C的方程;
(Ⅱ)求点P的坐标;
(Ⅲ)在y轴上求一点M,使M到曲线C上点的距离最大值为3
| 7 |
分析:(1)设G是曲线C上任意一点,依题意,|GE|+|GF|=12.a=6,c=4,b=
=
,由此可知所求的椭圆方程.
(2)由已知A(-6,0),F2(4,0),设点P的坐标为(x,y),则
=(x+6,y),
=(x-4,y)由已知得
则 2x2+9x-18=0,解之得x=
,或x=-6,由此可推导出点P的坐标为 (
,
);
(3)设圆M的圆心为(0,n),半径为3
,其方程为x2+(y-n)2=63,当此圆与椭圆相切时,使M到曲线C上点的距离最大值为3
.由此可推导出所求的M的坐标.
| 62-42 |
| 20 |
(2)由已知A(-6,0),F2(4,0),设点P的坐标为(x,y),则
| AP |
| FP |
|
| 3 |
| 2 |
| 3 |
| 2 |
5
| ||
| 2 |
(3)设圆M的圆心为(0,n),半径为3
| 7 |
| 7 |
解答:解:(1)设G是曲线C上任意一点,依题意,|GE|+|GF|=12.
所以曲线C是以E、F为焦点的椭圆,且椭圆的长半袖a=6,半焦距c=4,
所以短半轴 b=
=
,
所以所求的椭圆方程为
+
=1;
(2)由已知A(-6,0),F2(4,0),设点P的坐标为(x,y)
则
=(x+6,y),
=(x-4,y)
由已知得
则 2x2+9x-18=0,解之得x=
,或x=-6,
由于A,P两点不重合,所以只能取 x=
,于是y=
,
所以点P的坐标为 (
,
);
(3)设圆M的圆心为(0,n),半径为3
,其方程为x2+(y-n)2=63,当此圆与椭圆相切时,使M到曲线C上点的距离最大值为3
.
由
消去x得:
+
=1
则56y2+40ny+20n2-93=0.
△=0?n=6或8.
所求的M的坐标为(0,6)或(0,8).
所以曲线C是以E、F为焦点的椭圆,且椭圆的长半袖a=6,半焦距c=4,
所以短半轴 b=
| 62-42 |
| 20 |
所以所求的椭圆方程为
| x2 |
| 36 |
| y2 |
| 20 |
(2)由已知A(-6,0),F2(4,0),设点P的坐标为(x,y)
则
| AP |
| FP |
由已知得
|
则 2x2+9x-18=0,解之得x=
| 3 |
| 2 |
由于A,P两点不重合,所以只能取 x=
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
所以点P的坐标为 (
| 3 |
| 2 |
5
| ||
| 2 |
(3)设圆M的圆心为(0,n),半径为3
| 7 |
| 7 |
由
|
| 63-(y-n) 2 |
| 36 |
| y2 |
| 20 |
则56y2+40ny+20n2-93=0.
△=0?n=6或8.
所求的M的坐标为(0,6)或(0,8).
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细解答.解答的关键是利用方程思想设而不求进行解决直线和圆锥曲线的位置关系问题.

练习册系列答案
相关题目
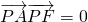 .
. ,若存在,求直线l的方程;若不存在,请说明理由.
,若存在,求直线l的方程;若不存在,请说明理由.