题目内容
曲线C上任一点到点E(-4,0),F(4,0)的距离的和为12,C与x轴的负半轴、正半轴依次交于A,B两点,点P在曲线C上且位于x轴上方,满足| PA |
| PF |
(1)求曲线C的方程;
(2)求点P的坐标;
(3)以曲线C的中心O为圆心,AB为直径作圆O,是否存在过点P的直线l使其被圆O所截的弦MN长为3
| 15 |
分析:(1)由题意知曲线C为椭圆且a=6,c=4得b2=20,由此能求出曲线C的方程.
(2)设P(x0,y0)又A(-6,0),F(4,0)且
•
=0,代入坐标得x02+2x0+y02-24=0,P在椭圆上故
+
=1,由P在x轴的上方得x0=
,y0=
,由此得到P点坐标.
(3)假设存在满足题意的直线l,若直线l得斜率不存在,则l:x=
;若直线l得斜率存在,设l:y-
=k(x-
),圆心到直线的距离d=
由题意知应有d=
,所以
=
得k=
,l:11x-5
y+21=0.
(2)设P(x0,y0)又A(-6,0),F(4,0)且
| PA |
| PF |
| ||
| 36 |
| ||
| 20 |
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
(3)假设存在满足题意的直线l,若直线l得斜率不存在,则l:x=
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
| 3 |
| 2 |
|3k-5
| ||
|
| 3 |
| 2 |
|3k-5
| ||
|
| 3 |
| 2 |
| 11 |
| 15 |
| 3 |
| 3 |
解答:解(1)由题意知曲线C为椭圆且a=6,c=4得b2=20
故曲线C的方程为
+
=1
(2)设P(x0,y0)又A(-6,0),F(4,0)且
•
=0
代入坐标得x02+2x0+y02-24=0①
又P在椭圆上故
+
=1②
由①②并P在x轴的上方得x0=
,y0=
所以P(
,
)
(3)假设存在满足题意的直线l10若直线l得斜率不存在,则l:x=
易得|MN|=3
,故满足题意.(9分)20若直线l得斜率存在,设l:y-
=k(x-
)
即2kx-2y-3k+5
=0
又圆心到直线的距离d=
由题意知应有d=
所以
=
得k=
则l:11x-5
y+21=0
综上得存在满足题意的直线:l:x=
或11x-5
y+21=0
故曲线C的方程为
| x2 |
| 36 |
| y2 |
| 20 |
(2)设P(x0,y0)又A(-6,0),F(4,0)且
| PA |
| PF |
代入坐标得x02+2x0+y02-24=0①
又P在椭圆上故
| ||
| 36 |
| ||
| 20 |
由①②并P在x轴的上方得x0=
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
所以P(
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
(3)假设存在满足题意的直线l10若直线l得斜率不存在,则l:x=
| 3 |
| 2 |
| 15 |
| 5 |
| 2 |
| 3 |
| 3 |
| 2 |
即2kx-2y-3k+5
| 3 |
又圆心到直线的距离d=
|3k-5
| ||
|
| 3 |
| 2 |
所以
|3k-5
| ||
|
| 3 |
| 2 |
| 11 |
| 15 |
| 3 |
则l:11x-5
| 3 |
综上得存在满足题意的直线:l:x=
| 3 |
| 2 |
| 3 |
点评:本题考查曲线方程的求法、求点P的坐标和判断直线方程是否存在,解题时要认真审题,注意合理地进行等价转化.本题计算量较大,比较繁琐,解题时要细心运算,避免出错.

练习册系列答案
相关题目
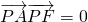 .
. ,若存在,求直线l的方程;若不存在,请说明理由.
,若存在,求直线l的方程;若不存在,请说明理由.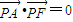 .
.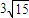 ,若存在,求直线l的方程;若不存在,请说明理由.
,若存在,求直线l的方程;若不存在,请说明理由.