题目内容
已知,![]() ,
,![]() 为
为![]() 的导数,
的导数,![]() .
.
(1)求![]() ,
,![]() ;
;
(2)若g(![]() )=
)=![]() -
-![]() -
-![]() ,求g(
,求g(![]() )的单调增区间;
)的单调增区间;
(3)解关于![]() 的不等式:
的不等式:![]() .
.
解:(1)![]() .
.
(2)![]() .
.
由g’(![]() )>0,得
)>0,得![]() <一1或
<一1或![]() >3.
>3.
∴g(![]() )的单调增区间是(一∞,一1),(3,+∞).
)的单调增区间是(一∞,一1),(3,+∞).
(3)不等式![]() 即为
即为![]() .
.
①当![]() >0时,显然有
>0时,显然有![]() >0.不等式化为
>0.不等式化为
![]() ,即
,即![]() ,∴
,∴![]() 且
且![]() .
.
∴0<![]() <2
<2![]() ,且
,且![]() ≠
≠![]() .
.
即![]() >0时,不等式的解为{
>0时,不等式的解为{![]() |0<
|0<![]() <2
<2![]() ,且
,且![]() ≠
≠![]() ).
).
②当![]() <0时,
<0时,![]() >0一定可使不等式成立.
>0一定可使不等式成立.
当![]() <0时,不等式化为
<0时,不等式化为![]() ,则
,则
![]() ∴
∴![]() .注意
.注意![]() <0,则解得
<0,则解得![]() <2
<2![]() .
.
∴当![]() <0时,不等式的解为{
<0时,不等式的解为{![]() |
|![]() <2
<2![]() ,或
,或![]() >0}.
>0}.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目

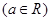 ,
, 为
为 的导数.
的导数.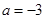 时,求
时,求 的单调区间和极值;
的单调区间和极值; ,是否存在实数
,是否存在实数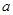 ,对于任意的
,对于任意的 ,存在
,存在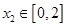 ,使得
,使得 成立?若存在,求出
成立?若存在,求出