题目内容
已知函数![]()
![]() ,
,![]() 为
为![]() 的导数。
的导数。
(I)当![]() =-3时证明
=-3时证明![]() 在区间(-1,1)上不是单调函数。
在区间(-1,1)上不是单调函数。
(II)设![]() ,是否存在实数
,是否存在实数![]() ,对于任意的
,对于任意的![]() 存在
存在![]() ,使得
,使得![]() 成立?若存在求出
成立?若存在求出![]() 的取值范围;若不存在说明理由。
的取值范围;若不存在说明理由。
解:(I)![]() 时
时 ![]()
![]() 其对标轴为
其对标轴为![]()
当![]() 时,
时,![]() 是单调增函数
是单调增函数
又![]() ,
,![]() 在(-1,1)上
在(-1,1)上![]()
在(-1,0)上![]() <0
<0 ![]() 为减函数
为减函数
在(0,1)上![]() >0
>0 ![]() 为增函数
为增函数
由上得出在(-1,1)上![]() 不是单调函数 ………………5分
不是单调函数 ………………5分
(II) 在[0,2]上![]() 是增函数,故对于
是增函数,故对于![]()
![]() ………………6分
………………6分
设![]()
![]()
![]() 由
由![]() 得
得![]() …………………7分
…………………7分
要使对于任意的![]() ,存在
,存在![]() 使得
使得![]() 成立
成立
只须在[-1,1]上-![]() ……………………………9分
……………………………9分
在(-1,-![]() )上
)上![]() 在(-
在(-![]() ,1)上
,1)上![]()
∴![]() 时
时 ![]() 有极小值
有极小值![]()
![]()
![]()
在[-1,1]上![]() 只有一个极小值数
只有一个极小值数 ![]() 最小值为
最小值为![]()

![]() ………………………………12分
………………………………12分

练习册系列答案
相关题目

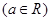 ,
, 为
为 的导数.
的导数.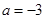 时,求
时,求 的单调区间和极值;
的单调区间和极值; ,是否存在实数
,是否存在实数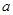 ,对于任意的
,对于任意的 ,存在
,存在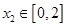 ,使得
,使得 成立?若存在,求出
成立?若存在,求出 在
在 处的导数为3,则
处的导数为3,则