Question

设P（x₀,y₀）是椭圆(a>b>0)上任意一点，F₁为其左焦点.

（1）求|PF₁|的最小值和最大值;

(2)在椭圆上求一点P，使这点与椭圆两焦点的连线互相垂直.

Answer 1

解:（1）对应于F₁的准线方程为x=，根据椭圆的第二定义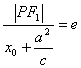：,∴|PF₁|=a+ex₀.又-a≤x₀≤a,

∴当x₀=-a时，|PF₁|_min=a+(-a)=a-c;

当x₀=a时，|PF₁|_max=a+·a=a+c.

(2)∵a²=25,b²=5,∴c²=20,e²=.

∵|PF₁|²+|PF₂|²=|F₁F₂|²,∴(a+ex₀)²+(a-ex₀)²=4c^2.将数据代入得25+=40.      

∴x₀=±.代入椭圆方程得P点的坐标为（,）.(,-),(-,)，(-,-).