Question

已知抛物线y²=6x，过点P(4，1)引一弦，使它恰在点P被平分，求这条弦所在的直线方程.

Answer 1

解法一:设直线上任意一点坐标为(x,y)，弦的两个端点为P₁(x₁,y₁)、P₂(x₂,y₂).

∵P₁、P₂在抛物线上，∴y₁²=6x₁,y₂²=6x₂.

两式相减得(y₁+y₂)(y₁-y₂)=6(x₁-x₂).①

∵y₁+y₂=2,代入①得.

∴直线的方程为y-1=3(x-4),

即3x-y-11=0.

解法二:设所求方程为y-1=k(x-4).

由方程组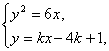

得ky²-6y-24k+6=0.

设弦的两端点P₁、P₂的坐标分别是(x₁,y₁)、(x₂,y₂)，

则

∵Ｐ₁Ｐ₂的中点为(4，1),∴.∴k=3.

∴所求直线方程为y-1=3(x-4)，即3x-y-11=0?

启示:解法一是求与中点有关问题常用的“作差法”，设点、作差、找斜率是重要的解题技巧.解法二没有求出P₁、P₂的坐标，而是运用韦达定理直接写出P₁P₂的中点坐标，这也是解题中常用的方法.一般求出直线方程后，把直线方程与抛物线方程联立，组成方程组看方程组是否有两解，有两解时求出的直线方程为所求直线方程，否则所求直线方程不存在.本例中的点P(4，1)在抛物线的张口内，不存在上述问题.