题目内容
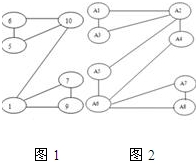 从0,1,2,…,10中挑选若干个不同的数字填满图中每一个圆圈称为一种“填法”,若各条线段相连的两个圆圈内的数字之差的绝对值各不相同,则称这样的填法为“完美填法”.
从0,1,2,…,10中挑选若干个不同的数字填满图中每一个圆圈称为一种“填法”,若各条线段相连的两个圆圈内的数字之差的绝对值各不相同,则称这样的填法为“完美填法”.试问:对图1和图2是否存在完美填法?若存在,请给出一种完美填法;若不存在,请说明理由.
分析:对于图1,各条线段相连的两个圆圈内的数字之差的绝对值各不相同,上述填法即为完美;对于图2不存在完美填法.利用反证法进行证明.假设存在完美填法.由于图中一共有10条连线,因此各连线上两数之差的绝对值恰好为1,2,3,…,10,其和s=55为奇数;另一方面,图中每一个圆圈所连接的连线数都为偶数条.即每一个圆圈内的数在上述S的表达式中出现偶数次.因此S应为偶数,出现矛盾.从而得出不存在完美填法.
解答:解:对图1,上述填法即为完美(答案不唯一).…(10分)
对于图2不存在完美填法.因为图中一共有10条连线,因此各连线上两数之差的绝对值恰好为1,2,3,…,10,…(15分)
其和s=|a1-a2|+|a1-a3|+|a2-a3|+…+|a7-a8|=55为奇数.…(20分)
另一方面,图中每一个圆圈所连接的连线数都为偶数条.
即每一个圆圈内的数在上述S的表达式中出现偶数次.因此S应为偶数,矛盾.…(25分)
所以,不存在完美填法.
对于图2不存在完美填法.因为图中一共有10条连线,因此各连线上两数之差的绝对值恰好为1,2,3,…,10,…(15分)
其和s=|a1-a2|+|a1-a3|+|a2-a3|+…+|a7-a8|=55为奇数.…(20分)
另一方面,图中每一个圆圈所连接的连线数都为偶数条.
即每一个圆圈内的数在上述S的表达式中出现偶数次.因此S应为偶数,矛盾.…(25分)
所以,不存在完美填法.
点评:本小题主要考查进行简单的合情推理等基础知识,考查运算求解能力,考查数形结合思想、反证法思想.属于中档题.

练习册系列答案
相关题目

