题目内容
实系数一元二次方程x2-ax+2b=0的两根分别在区间(0,1)和(1,2)上,则2a+3b的取值范围是________.
(2,9)
分析:先根据实系数一元二次方程x2-ax+2b=0的两根分别在区间(0,1)和(1,2)上,得到线性约束条件,画出可行域,把特殊点坐标代入即可求出结论.
解答:设f(x)=x2-ax+2b,
因为实系数一元二次方程x2-ax+2b=0的两根分别在区间(0,1)和(1,2)上,
所以: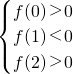 ?
? .
.

由图得:Z=2a+3b过点B(1,0)时取最小值2,过点A(3,1)时取最大值9.
又因为不含边界,
故2a+3b∈(2,9).
故答案为:(2,9).
点评:本题主要考查了一元二次方程根的分布问题以及简单的线性规划,利用几何意义求最值,是对基础知识的综合考查.
分析:先根据实系数一元二次方程x2-ax+2b=0的两根分别在区间(0,1)和(1,2)上,得到线性约束条件,画出可行域,把特殊点坐标代入即可求出结论.
解答:设f(x)=x2-ax+2b,
因为实系数一元二次方程x2-ax+2b=0的两根分别在区间(0,1)和(1,2)上,
所以:
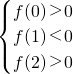 ?
? .
.
由图得:Z=2a+3b过点B(1,0)时取最小值2,过点A(3,1)时取最大值9.
又因为不含边界,
故2a+3b∈(2,9).
故答案为:(2,9).
点评:本题主要考查了一元二次方程根的分布问题以及简单的线性规划,利用几何意义求最值,是对基础知识的综合考查.

练习册系列答案
相关题目
已知实系数一元二次方程x2+(1+a)x+a+b+1=0的两个实根为x1,x2,且 0<x1<1,x2>1,则
的取值范围是( )
| b |
| a |
A、(-1,-
| ||
B、(-1,-
| ||
C、(-2,-
| ||
D、(-2,-
|