题目内容
F1,F2为椭园 的左右焦点,l是它的一条准线,点P在l上,则∠F1PF2的最大值为________.
的左右焦点,l是它的一条准线,点P在l上,则∠F1PF2的最大值为________.

分析:椭圆
 的准线方程:x=-2
的准线方程:x=-2 ,设P(-2
,设P(-2 ,y0),y0≠0设直线PF1的斜率k1=
,y0),y0≠0设直线PF1的斜率k1= ,直线PF2的斜率k2=
,直线PF2的斜率k2= ,由题设知∠F1PF为锐角.由此能导出∠F1PF2的最大值.
,由题设知∠F1PF为锐角.由此能导出∠F1PF2的最大值.解答:
 解:椭圆
解:椭圆 的准线方程:x=-2
的准线方程:x=-2 ,
,设P(-2
 ,y0),y0≠0设直线PF1的斜率k1=
,y0),y0≠0设直线PF1的斜率k1= ,直线PF2的斜率k2=
,直线PF2的斜率k2= ,
,∵
 ,∴∠F1PF2为锐角.
,∴∠F1PF2为锐角.tan∠F1PF2=|
 |=|
|=| |=
|= ≤
≤ ,
,当
 ,即
,即  时,tan∠F1PF2取到最大值,
时,tan∠F1PF2取到最大值,此时∠F1PF2最大,故∠F1PF2的最大值为
 .
.故答案为:
 .
.点评:本题考查直线与圆锥曲线的位置关系,解题时要认真审题,仔细求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知椭圆
已知椭圆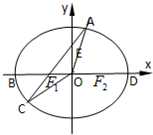 (A题)如图,在椭圆
(A题)如图,在椭圆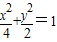 的左右焦点,l是它的一条准线,点P在l上,则∠F1PF2的最大值为 .
的左右焦点,l是它的一条准线,点P在l上,则∠F1PF2的最大值为 .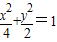 的左右焦点,l是它的一条准线,点P在l上,则∠F1PF2的最大值为 .
的左右焦点,l是它的一条准线,点P在l上,则∠F1PF2的最大值为 .