题目内容
如图2-5-14,以⊙O上的一点A为圆心作⊙A,分别交⊙O于B、C,过A作弦AF交公共弦于E,交⊙A于D.求证:AD2=AE·AF.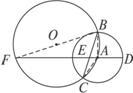
图2-5-14
思路分析:由于本题要证的成比例的四条线段在同一条直线上,因此不存在相似三角形,所以必须转移其中一条或两条,以构成两个能够相似的三角形,注意到同圆半径相等的性质,所以将AD换成AB,通过等线段代换,可以达到目的.

证明:分别连结![]() 、
、![]() 、BF.
、BF.
∵AB=AC,∴AB=AC.
∴∠ABC=∠F.
又∠BAF公共,∴△ABE∽△BFA.
∴AB2=AE·AF.
∵AB=AD,∴AD2=AE·AF.

练习册系列答案
相关题目
 21、某校高三年级800名学生参加英语口语测试,将精确到0.1分的成绩分成5组,绘成频率分布直方图如图,且知第1,2,3,5小组的频率分别为0.04,0.14,0.26,0.28.
21、某校高三年级800名学生参加英语口语测试,将精确到0.1分的成绩分成5组,绘成频率分布直方图如图,且知第1,2,3,5小组的频率分别为0.04,0.14,0.26,0.28. 本题有(1),(2),(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑.
本题有(1),(2),(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑.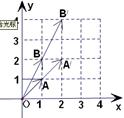
 被矩阵M作用后分别变成
被矩阵M作用后分别变成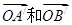 ,
,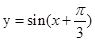 在M作用后的函数解析式;
在M作用后的函数解析式;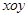 中,直线
中,直线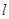 的参数方程为
的参数方程为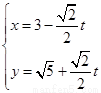 (
(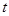 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系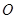 为极点,以
为极点,以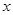 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为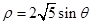 。
。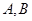 。若点
。若点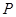 的坐标为(3,
的坐标为(3,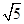 ),求
),求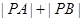 。
。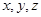 为正实数,且
为正实数,且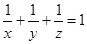 ,求
,求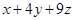 的最小值及取得最小值时
的最小值及取得最小值时