题目内容
盒中装着标有数字1、2、3、4的小球各2个,从盒中任意摸一次,同时取出3个小球,每个小球被取到的可能性都相等,求:
(1)取出的3个小球上最大的数字是4的概率;
(2)取出的3个小球中有2个小球上的数字是3的概率;
(3)取出的3个小球上的数字的互不相同的概率.
解:从盒中任意摸一次,同时取出3个小球,且每个小球被取到的可能性都相等,
由此可得所有的基本事件共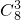 =56个.
=56个.
(1)记事件A=“取出的3个小球上最大的数字是4”,共有两类:
①3个球中有1个为4,另一个不是4,有 =15个基本事件;
=15个基本事件;
①3个球中有2个为4,另一个不是4,6个基本事件.
故符合题意的基本事件总数为15+6=21个
∴所求的概率为P(A)=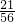 =
= .
.
(2)记事件B=“取出的3个小球中有2个小球上的数字是3”,
符合题意的基本事件总共6个
∴所求的概率为P(B)=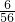 =
=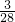 .
.
(3)记事件C=“取出的3个小球上的数字的互不相同”,
符合题意的基本事件总共: =32个
=32个
∴所求的概率为P(C)= =
= .
.
答:(1)取出的3个小球上最大的数字是4的概率为 ;
;
(2)取出的3个小球中有2个小球上的数字是3的概率为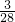 ;
;
(3)取出的3个小球上的数字的互不相同的概率为 .
.
分析:从盒中任意摸一次,同时取出3个小球,且每个小球被取到的可能性都相等,由此可得所有的基本事件共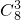 =56个.
=56个.
(1)符合题意的基本事件分为两类:①有且只有一个4,此时只要在标有1、2、3的六个球中选2个,共 =15种情况;②有2个4,此时只要在标有1、2、3的六个球中选1个,共6种情况,再用等可能性事件的概率公式,可得所求的概率;
=15种情况;②有2个4,此时只要在标有1、2、3的六个球中选1个,共6种情况,再用等可能性事件的概率公式,可得所求的概率;
(2)符合题意的基本事件:在标有1、2、4的六个球中选1个,共6种情况,再用等可能性事件的概率公式,可得所求的概率;
(3)符合题意的基本事件:先从1、2、3、4四个数中选三个不相同的数,然后分别在相应数字的球中2选1,共 =32种情况,再用等可能性事件的概率公式,可得所求的概率.
=32种情况,再用等可能性事件的概率公式,可得所求的概率.
点评:本题借助于一个摸球的实际问题为载体,着重考查了排列与组合公式、等可能性事件的概率和乘法原理等知识点,属于中档题.
由此可得所有的基本事件共
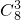 =56个.
=56个.(1)记事件A=“取出的3个小球上最大的数字是4”,共有两类:
①3个球中有1个为4,另一个不是4,有
 =15个基本事件;
=15个基本事件;①3个球中有2个为4,另一个不是4,6个基本事件.
故符合题意的基本事件总数为15+6=21个
∴所求的概率为P(A)=
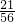 =
= .
.(2)记事件B=“取出的3个小球中有2个小球上的数字是3”,
符合题意的基本事件总共6个
∴所求的概率为P(B)=
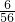 =
=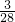 .
.(3)记事件C=“取出的3个小球上的数字的互不相同”,
符合题意的基本事件总共:
 =32个
=32个∴所求的概率为P(C)=
 =
= .
.答:(1)取出的3个小球上最大的数字是4的概率为
 ;
;(2)取出的3个小球中有2个小球上的数字是3的概率为
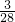 ;
;(3)取出的3个小球上的数字的互不相同的概率为
 .
.分析:从盒中任意摸一次,同时取出3个小球,且每个小球被取到的可能性都相等,由此可得所有的基本事件共
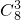 =56个.
=56个.(1)符合题意的基本事件分为两类:①有且只有一个4,此时只要在标有1、2、3的六个球中选2个,共
 =15种情况;②有2个4,此时只要在标有1、2、3的六个球中选1个,共6种情况,再用等可能性事件的概率公式,可得所求的概率;
=15种情况;②有2个4,此时只要在标有1、2、3的六个球中选1个,共6种情况,再用等可能性事件的概率公式,可得所求的概率;(2)符合题意的基本事件:在标有1、2、4的六个球中选1个,共6种情况,再用等可能性事件的概率公式,可得所求的概率;
(3)符合题意的基本事件:先从1、2、3、4四个数中选三个不相同的数,然后分别在相应数字的球中2选1,共
 =32种情况,再用等可能性事件的概率公式,可得所求的概率.
=32种情况,再用等可能性事件的概率公式,可得所求的概率.点评:本题借助于一个摸球的实际问题为载体,着重考查了排列与组合公式、等可能性事件的概率和乘法原理等知识点,属于中档题.

练习册系列答案
相关题目