题目内容
已知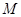 为椭圆
为椭圆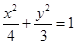 上一点,
上一点,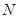 为椭圆长轴上一点,
为椭圆长轴上一点,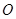 为坐标原点.
为坐标原点.
给出下列结论:
①存在点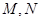 ,使得
,使得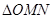 为等边三角形;
为等边三角形;
②不存在点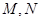 ,使得
,使得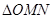 为等边三角形;
为等边三角形;
③存在点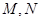 ,使得
,使得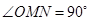 ;
;
④不存在点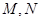 ,使得
,使得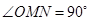 .
.
其中,所有正确结论的序号是__________.
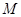 为椭圆
为椭圆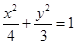 上一点,
上一点,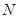 为椭圆长轴上一点,
为椭圆长轴上一点,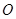 为坐标原点.
为坐标原点.给出下列结论:
①存在点
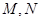 ,使得
,使得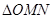 为等边三角形;
为等边三角形;②不存在点
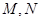 ,使得
,使得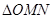 为等边三角形;
为等边三角形;③存在点
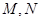 ,使得
,使得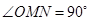 ;
;④不存在点
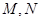 ,使得
,使得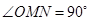 .
.其中,所有正确结论的序号是__________.
①④
试题分析:若过存在点
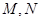 ,使得
,使得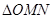 为等边三角形,由椭圆的对称性设
为等边三角形,由椭圆的对称性设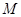 点在第一象限
点在第一象限 .代入椭圆方程可得
.代入椭圆方程可得 .解得
.解得 .所以
.所以 .所以存在点
.所以存在点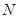 .所以①正确;若存在点
.所以①正确;若存在点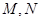 ,使得
,使得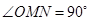 ,同样设
,同样设 ,代入椭圆方程可得
,代入椭圆方程可得 ,解得
,解得 .所以
.所以
 .所以不存在点
.所以不存在点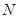 .所以④正确.故填①④.
.所以④正确.故填①④.
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
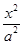 +
+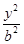 =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点.若AB的中点坐标为(1,-1),则E的方程为( ).
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点.若AB的中点坐标为(1,-1),则E的方程为( ).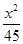 +
+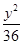 =1 B.
=1 B.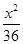 +
+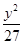 =1
=1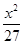 +
+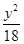 =1 D.
=1 D.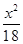 +
+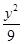 =1
=1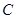 :
: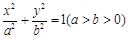 的短轴长为2,离心率为
的短轴长为2,离心率为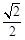 ,设过右焦点的直线
,设过右焦点的直线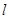 与椭圆
与椭圆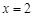 的垂线AP,BQ,垂足分别为P,Q.记
的垂线AP,BQ,垂足分别为P,Q.记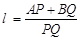 , 若直线l的斜率
, 若直线l的斜率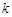 ≥
≥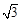 ,则
,则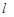 的取值范围为 .
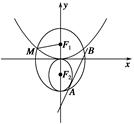
的取值范围为 .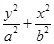 =1(a>b>0)的上下焦点,其中F1是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=
=1(a>b>0)的上下焦点,其中F1是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=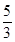 .
.
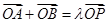 ,求实数λ的取值范围.
,求实数λ的取值范围.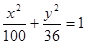 的焦距等于( )
的焦距等于( ) ,
, 是椭圆
是椭圆 的左、右焦点,过
的左、右焦点,过 两点,若△
两点,若△ 的周长为
的周长为 ,则
,则 的值为 .
的值为 .
 的左、右焦点分别为
的左、右焦点分别为 ,
, 是
是 上两点,
上两点, ,
, ,则椭圆
,则椭圆



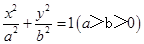 的右焦点为F,其右准线与
的右焦点为F,其右准线与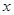 轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点F,则椭圆离心率的取值范围是( )
轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点F,则椭圆离心率的取值范围是( )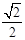 ]
]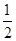 ]
]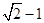 ,1)
,1)