题目内容
设
是整数集
的非空子集，如果
有
，则称
关于数的乘法是封闭的. 若
,
是的两个不相交的非空子集，
且
有
有
，有四个命题：①
中至少有一个关于乘法是封闭的；②中至多有一个关于乘法是封闭的;③中有且只有一个关于乘法是封闭的；④中每一个关于乘法都是封闭的.其中所有正确命题的序号是 .
①
解析试题分析：因为关于乘法封闭的规定是.是整数集的非空子集，如果有，则称关于数的乘法是封闭的.如果代表负数集合，代表非负数集合，则成立, 且有有.但是
.所以不是乘法封闭.所以④不正确. 如果代表奇数集合，代表偶数集合，则成立, 且有有.显然
都是乘法封闭的，所以②③都不正确. 若都不满足乘法封闭，有
.假设
，若存在，则
与题意矛盾.所以①正确.故填①
考点：1.集合的概念.2.新定义的概念的理解.3.列举特值解题的思想.
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
的定义域为
；②
；③函数
的图像关于点
对称；④若角的集合
,
,则
；⑤函数
的最小正周期是
,对称轴方程为直线
.其中正确结论的序号是 _______. 
，
，若
，则实数
的取值范围是 ．
表示集合S中的元素的个数，设
为集合，称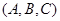
为有序三元组．如果集合
，且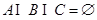
，则称有序三元组
的子集构成的所有有序三元组中，最小相交的有序三元组的个数为 ．
中任取一个元素，所取元素恰好满足方程
的概率是_________．
，
.
1时，求集合
；
时，求
的取值范围．给出下列关系：①
； ②
；③ 
；④
. 其中正确的个数是( )
| A．1 | B．2 | C．3 | D．4 |
,
},则
= .