题目内容
已知函数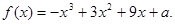
(1)求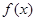 的单调减区间;
的单调减区间;
(2)若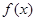 在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
【答案】
(1)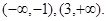
(2)-7
【解析】本试题主要是考查了导数在研究函数中的运用,运用导数的正负来判定增减性,以及求解给定闭区间上的最值问题。
解:(I)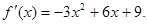 令
令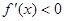 ,解得
,解得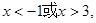 -----------4分
-----------4分
所以函数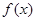 的单调递减区间为
的单调递减区间为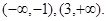 -------------------------6分
-------------------------6分
(II)因为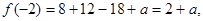
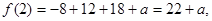
所以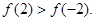 -------------------------------------------8分
-------------------------------------------8分
因为在(-1,3)上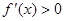 ,所以
,所以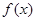 在[-1,2]上单调递增,又由于
在[-1,2]上单调递增,又由于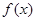 在
在
[-2,-1]上单调递减,因此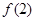 和
和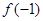 分别是
分别是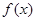 在区间[-2,2]上的最大值和最小值.于是有
在区间[-2,2]上的最大值和最小值.于是有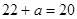 ,解得
,解得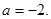 ----------------10分
----------------10分
故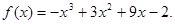 因此
因此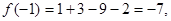
即函数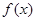 在区间[-2,2]上的最小值为-7.
在区间[-2,2]上的最小值为-7.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 的最小正周期及
的最小正周期及 上的图象.
上的图象. ,
,
 的单调区间;
的单调区间;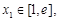 ,都存在
,都存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。 知函数
知函数
 的定义域;
的定义域; 上是减函数.
上是减函数. .
. 的最小正周期;
的最小正周期; 上的最大值和最小值以及取得最大值、最小值时x的值.
上的最大值和最小值以及取得最大值、最小值时x的值.