题目内容
若f(x)=x2-2x-4lnx,不等式f′(x)>0的解集为p,关于x的不等式x2+(a-1)x-a>0的解集记为q,已知p是q的充分不必要条件,则实数a的取值范围是( )A.(-2,-1]
B.[-2,-1]
C.∅
D.[-2,+∞)
【答案】分析:分别求解解集p与q,由p是q的充分不必要条件可知p是q的真子集,利用集合的包含关系可以求得.
解答:解:不等式f′(x)>0即
2x-2-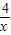 >0(其中x>0)的解集p为(2,+∞),
>0(其中x>0)的解集p为(2,+∞),
不等式x2+(a-1)x-a>0可化为(x-1)(x+a)>0,
由于p是q的充分不必要条件可知p是q的真子集,
①当-a<1时,不等式x2+(a-1)x-a>0的解集为(-∞,-a)∪(1,+∞),此时满足题意;
②当-a=1时,不等式x2+(a-1)x-a>0的解集为(-∞,1)∪(1,+∞),此时满足题意;
③当-a>1时,不等式x2+(a-1)x-a>0的解集为(-∞,1)∪(-a,+∞),必须有-a≤2,即-1<a≤-2.
∴实数a的取值范围是[-2,+∞).
故选D.
点评:本题重点考查四种条件,考查集合之间的包含关系,利用集合的包含关系解决有关四种条件问题是一种行之有效的方法,注意细细体会.
解答:解:不等式f′(x)>0即
2x-2-
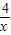 >0(其中x>0)的解集p为(2,+∞),
>0(其中x>0)的解集p为(2,+∞),不等式x2+(a-1)x-a>0可化为(x-1)(x+a)>0,
由于p是q的充分不必要条件可知p是q的真子集,
①当-a<1时,不等式x2+(a-1)x-a>0的解集为(-∞,-a)∪(1,+∞),此时满足题意;
②当-a=1时,不等式x2+(a-1)x-a>0的解集为(-∞,1)∪(1,+∞),此时满足题意;
③当-a>1时,不等式x2+(a-1)x-a>0的解集为(-∞,1)∪(-a,+∞),必须有-a≤2,即-1<a≤-2.
∴实数a的取值范围是[-2,+∞).
故选D.
点评:本题重点考查四种条件,考查集合之间的包含关系,利用集合的包含关系解决有关四种条件问题是一种行之有效的方法,注意细细体会.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目