题目内容
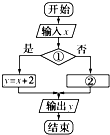
 如图,流程图表示的是输出100以内(不含100)除以3余1的正整数的算法,则应在判断框内填入的循环终止条件是( )
如图,流程图表示的是输出100以内(不含100)除以3余1的正整数的算法,则应在判断框内填入的循环终止条件是( )分析:根据程序的功能是输出100以内(不含100)除以3余1的正整数的算法,而每次循环变量值增加1,故每次输出的应为3n+1,而条件应该是输出最后一个a值97,此时对应的n值为32时,第一次满足.
解答:解:∵根据程序的功能是输出100以内(不含100)除以3余1的正整数的算法,
循环变量的初值为1,步长为1
故每次输出的应该是循环变量n的3倍加1,
故a=7n+1;
又程序在运行过程中各变量的值如下表示:
依此类推,我们需要计算满足3k+1≥100的最小正整数k,可得k≥33,
符合题意最小正整数33
故判断框中应该填上“n≥33”.
故选D.
循环变量的初值为1,步长为1
故每次输出的应该是循环变量n的3倍加1,
故a=7n+1;
又程序在运行过程中各变量的值如下表示:
| n | a | 是否继续循环 | |
| 循环前 | 0 | / | 执行 |
| 第一圈 | 1 | 1 | 执行 |
| 第二圈 | 2 | 4 | 执行 |
| … | … | 执行 | |
| 第k圈 | k | 3k-2 |
符合题意最小正整数33
故判断框中应该填上“n≥33”.
故选D.
点评:根据流程图(或伪代码)写程序的运行结果或在判断框填上符合条件的式子,是算法这一模块常见的题型.其基本处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中分析出计算的类型;②建立数学模型,根据第一步分析的结果,选择恰当的数学模型;③解模.

练习册系列答案
相关题目
 已知函数f(x)=
已知函数f(x)= 如图,流程图表示的是输出100以内(不含100)除以3余1的正整数的算法,则应在判断框内填入的循环终止条件是
如图,流程图表示的是输出100以内(不含100)除以3余1的正整数的算法,则应在判断框内填入的循环终止条件是