题目内容
已知函数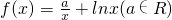 .
.
(1)讨论f(x)的单调性及极值;
(2)设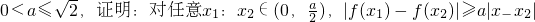 .
.
解:(1)由
①当a≤0时,f′(x)>0,故f(x)在(0,+∞)上单调递增,无极值;
②当a>0时,若0<x<a,f′(x)<0,故函数f(x)在(0,a)上单调递减,
若x>a,f′(x)>0,故f(x)在(a,+∞)上单调递增,
所以极小值f(a)=1+lna,无极大值.
(2)证明:不妨设x1≥x2,而0<a ,由(1)知f(x)在(0,
,由(1)知f(x)在(0, )的单调递减,
)的单调递减,
故对任意 ,|f(x1)-f(x2)|≥a|x1-x2|等价于:
,|f(x1)-f(x2)|≥a|x1-x2|等价于:

即f(x1)+ax1≤f(x2)+ax2
令g(x)=f(x)+ax,则 ,
,
令h(x)=ax2+x-a,∵0<a ,
,
∴h(0)=-a<0, ,
,
则 ,故g(x)在(0,
,故g(x)在(0, )上单调递减,
)上单调递减,
又由x1≥x2,∴g(x2)≥g(x1),即f(x2)+ax2≥f(x1)+ax1
∴ .
.
分析:(1)借助于导数,讨论参数,得到函数的单调区间和极值;
(2)借助于(1)的单调区间可知函数在(0, )的单调性,构建新函数,再借助其导数,判断新函数的单调性,即得证.
)的单调性,构建新函数,再借助其导数,判断新函数的单调性,即得证.
点评:本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

①当a≤0时,f′(x)>0,故f(x)在(0,+∞)上单调递增,无极值;
②当a>0时,若0<x<a,f′(x)<0,故函数f(x)在(0,a)上单调递减,
若x>a,f′(x)>0,故f(x)在(a,+∞)上单调递增,
所以极小值f(a)=1+lna,无极大值.
(2)证明:不妨设x1≥x2,而0<a
 ,由(1)知f(x)在(0,
,由(1)知f(x)在(0, )的单调递减,
)的单调递减,故对任意
 ,|f(x1)-f(x2)|≥a|x1-x2|等价于:
,|f(x1)-f(x2)|≥a|x1-x2|等价于:
即f(x1)+ax1≤f(x2)+ax2
令g(x)=f(x)+ax,则
 ,
,令h(x)=ax2+x-a,∵0<a
 ,
,∴h(0)=-a<0,
 ,
,则
 ,故g(x)在(0,
,故g(x)在(0, )上单调递减,
)上单调递减,又由x1≥x2,∴g(x2)≥g(x1),即f(x2)+ax2≥f(x1)+ax1
∴
 .
.分析:(1)借助于导数,讨论参数,得到函数的单调区间和极值;
(2)借助于(1)的单调区间可知函数在(0,
 )的单调性,构建新函数,再借助其导数,判断新函数的单调性,即得证.
)的单调性,构建新函数,再借助其导数,判断新函数的单调性,即得证.点评:本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

练习册系列答案
相关题目
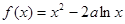 ,
,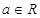
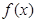 单调区间;
单调区间;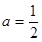 时,证明:当
时,证明:当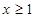 时,证明:
时,证明: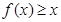 。
。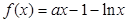
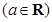 .
.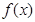 在定义域内的极值点的个数;
在定义域内的极值点的个数; 处取得极值,对
处取得极值,对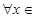
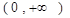 ,
,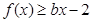 恒成立,求实数
恒成立,求实数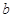 的取值范围.
的取值范围. 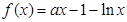
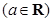 .
.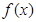 在定义域内的极值点的个数;
在定义域内的极值点的个数;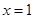 处取得极值,对
处取得极值,对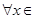
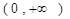 ,
,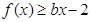 恒成立,求实数
恒成立,求实数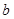 的取值范围;
的取值范围;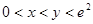 且
且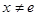 时,试比较
时,试比较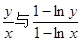 的大小.
的大小. .
. 函数
函数 的单调性;
的单调性; 为偶数时,正项数列
为偶数时,正项数列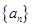 满足
满足 ,求
,求 时,求证:
时,求证: .
. 。(1)讨论函数
。(1)讨论函数 的单调性;(2)当
的单调性;(2)当 时,设
时,设 ,若
,若 时,
时, 恒成立。求整数
恒成立。求整数 的最大值。
的最大值。