Question

(理)对数列{a_n}和{b_n}，若对任意正整数n，恒有b_n≤a_n，则称数列{b_n}是数列{a_n}的“下界数列”．

(1)设数列a_n＝2n＋1，请写出一个公比不为1的等比数列{b_n}，使数列{b_n}是数列{a_n}的“下界数列”；

(2)设数列，求证数列{b_n}是数列{a_n}的“下界数列”；

(3)设数列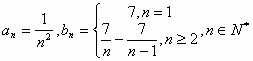，构造，，求使对恒成立的k的最小值．

Answer 1

答案：
解析：

　　(理)

　　(1)等，答案不唯一　　4分

　　(2)，当时最小值为9　　6分

　　，则，

　　因此，时，最大值为6　　9分

　　所以，，数列是数列的“下界数列”　　10分

　　(3)

　　　　11分

　　　　12分

　　不等式为，，　　13分

　　设，则　　15分

　　当时，单调递增，时，取得最小值，因此　　17分

　　的最小值为　　18分