题目内容
已知数列{an}，{bn}是各项均为正数的等比数列，设cn=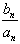
（n∈N*），
（Ⅰ）数列{cn}是否为等比数列？证明你的结论；
（Ⅱ）设数列{lnan}，{lnbn}的前n项和分别为Sn，Tn，若a1=2，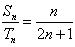
，求数列{cn}的前n项和。
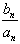（n∈N*）， （Ⅰ）数列{cn}是否为等比数列？证明你的结论；
（Ⅱ）设数列{lnan}，{lnbn}的前n项和分别为Sn，Tn，若a1=2，
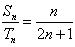，求数列{cn}的前n项和。 解：（Ⅰ）{cn}为等比数列；
证明：设{an}的公比为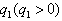
，{bn}的公比为
，
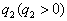则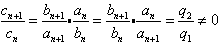
，
故{cn}为等比数列．
（Ⅱ）数列{lnan}和{lnbn}分别是公差为
的等差数列，
由条件得
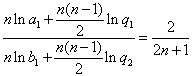，即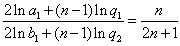
，
故对n=1，2，…，
，
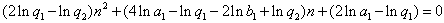于是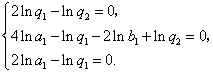
将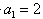
代入得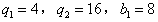
，
从而有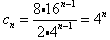
，
所以数列{cn}的前n项和为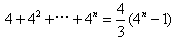
。
证明：设{an}的公比为
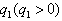，{bn}的公比为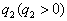，则
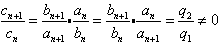，故{cn}为等比数列．
（Ⅱ）数列{lnan}和{lnbn}分别是公差为
的等差数列，由条件得
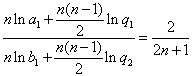，即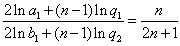，故对n=1，2，…，
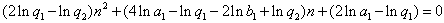，于是
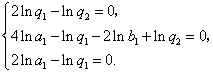
将
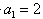代入得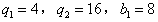，从而有
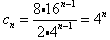，所以数列{cn}的前n项和为
。
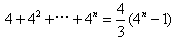练习册系列答案
相关题目