题目内容
(满分14分)![]() 是首项
是首项![]() 的等比数列,且
的等比数列,且![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,设
,设![]() 为数列
为数列 的前
的前![]() 项和,若
项和,若![]() ≤
≤![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的最小值.
的最小值.
(满分14分)解: (1)∵![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,
∴![]() ,即
,即![]() ,所以
,所以![]() ,
,
∵![]() , ∴
, ∴![]() .
.
∴![]() .
.
(2)∵![]() =
=![]() ,
,
∴![]() =
=![]()
=![]()
=![]() .
.
又![]() ≤
≤![]() ,即
,即![]()
![]()
所以, ![]()
![]() 对一切
对一切![]() 恒成立.
恒成立.
∵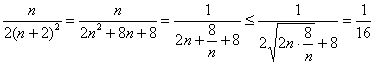 .
.
∴实数![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是首项
是首项 的等比数列,且
的等比数列,且 ,
,
 ,
, 成等差数列,
成等差数列, ,设
,设 为数列
为数列 的前
的前 项和,若
项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值. 是首项
是首项 的等比数列,且
的等比数列,且 ,
, ,
, 成等差数列,
成等差数列, ,设
,设 为数列
为数列 的前
的前 项和,若
项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.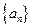 是首项
是首项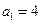 的等比数列,且
的等比数列,且 ,
,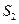 ,
,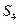 成等差数列,
成等差数列, ,设
,设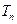 为数列
为数列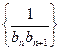 的前
的前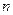 项和,若
项和,若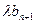 对一切
对一切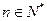 恒成立,求实数
恒成立,求实数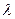 的最小值.
的最小值.